3dvi

论文名：Normalization and de-noising of scHi-C data with BandNorm and scVI-3D

introduction

主要使用了两种方法，BandNorm和scVI-3D。分别解决了scHi-C数据的normalization和de-noising问题。我们关心的主要的还是scVI-3D模型。

• 数据

Hi-C的数据天生的具有一些bias和noise，比如systematic genomic distance bias，这些噪声由测序的实验引起，很难改进，给下游的分析任务带来很大的困扰。而single cell数据相对于集群细胞的数据而言，又天生的具有稀疏性和噪声。相对于其他的single cell数据，scHi-C数据由于使用了基因组的绝对坐标作为基本的研究单元，所以更加的稀疏。

• 方法

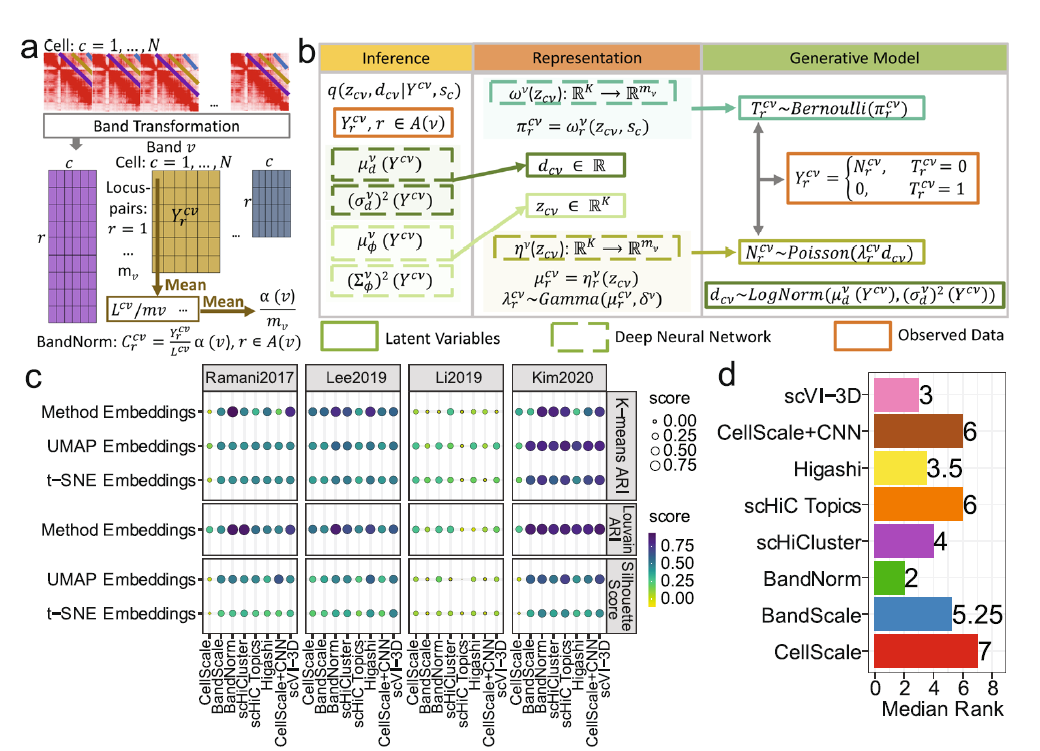
fig-1a介绍了bandnorm方法。在进行bandnorm之前，首先将接触矩阵拆分成band-specific cell 和 基因座矩阵（感觉意思就是把数据拆成每个细胞）。然后再每个细胞的每条染色体上分别进行bandnorm，将原始的接触系数$Y_{r}^{cv}$(r:基因座；v:Band，感觉意思就是bin后的接触矩阵的坐标；c:cell)。bandnorm的公式是：

$$C_{r}^{cv} = \frac{Y_{r}^{cv}}{L^{cv}}\alpha(v)$$

fig-1b介绍了scVI-3D模型。将$Y{r}^{cv}$投射为隐层变量$z{cv}$…说是让看后边的详细介绍，最关心的就是这一部分，但是这部分最语焉不详。

fig-1c和fig-1d介绍了几种方法的对比，CellScale, BandScale, BandNorm, scHiCluster, scHiC Topics, Higashi, CellScale+CNN, scVI-3D。分别在Ramani2017, Lee2019, Li2019, Kim2020数据集上进行了测试。不是我们关心的部分。

接下来直接跳到论文的第23页看他的scVI-3D模型。

scVI-3D模型

scVI-3D模型将基因座之间的交互频率建模为从零膨胀负二项分布(zero-inflated negative binomial distribution)中得到的采样，同时考虑library size和batch effect。

整体上跟用于scRNA-seq的scVI差距不大，模型的本质是一个VAE模型。原始的VAE模型中认为变量服从高斯分布，使用神经网络学习$\mu和\sigma$。这里的scVI认为输入的数据服从的是零膨胀负二项分布，使用神经网络学习$\theta, r和p$。

---

零膨胀负二项分布

在介绍零膨胀负二项分布之前，首先介绍一下为什么要使用这样一个分布对交互频率进行建模。之前介绍过，single cell数据天然的具有很高的稀疏性，而且，由于测序数据事实上就是基因座之间的交互频率，这些数据的取值必然是非负整数。很自然的，我们就可以想到使用Poisson分布对scHiC数据进行建模。

• 泊松分布
  泊松分布的概率密度函数如下所示： $$f(k;\lambda) = P(X = k) = \frac{\lambda^{k}e^{-\lambda}}{k!}$$

使用泊松分布描述scHiC数据的问题在于，对于一个泊松分布来说，他的期望和方差是相等的，即$E(X) = Var(X) = \lambda$。但是对于实际的单细胞数据而言，随着基因的表达水平的越高，其样本方差和样本均值的差就越大。即所谓的过度分散性。所以使用泊松分布是不合时宜的。参考scRNA-seq的一些相关解释。引入Gamma分布。

• Gamma分布
  Gamma分布的概率密度函数如下所示：

$$f(x ; \alpha, \beta)=\frac{\beta^{\alpha} x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)} \quad \text { for } x>0 \quad \alpha, \beta>0$$

Poisson分布的$\lambda$是不变的，但是，这样的Poisson分布不能满足我们的要求，因此，我们引入一个先验，即：

$$\lambda \sim \Gamma(r, \frac{1-p}{p})$$

不知道为什么要这样做，但是这时，问题可以描述为：

$$X \sim Poisson(\lambda) \\ \lambda \sim \Gamma(r, \frac{1-p}{p}) \quad r>0,0<p<1$$

• 负二项分布
  这时，可以证明X服从负二项分布(negative binomial distribution)。 $$\begin{aligned} P(X=x) &=\int_{0}^{\infty} P(x \mid \lambda) P(\lambda) d \lambda \\ &=\int_{0}^{\infty} \frac{\lambda^{x} e^{-\lambda}}{x !} \frac{\left(\frac{1-p}{P}\right)^{r}}{\Gamma(r)} \lambda^{r-1} e^{-\frac{\lambda(1-p)}{p}} d \lambda \\ &=\frac{\left(\frac{1-p}{p}\right)^{r}}{x ! \Gamma(r)} \int_{0}^{\infty} \lambda^{x+r-1} e^{-\frac{\lambda}{p}} d \lambda \\ &=\frac{\left(\frac{1-p}{p}\right)^{r}}{x ! \Gamma(r)}(p)^{x+r} \Gamma(x+r) \\ &=\frac{\Gamma(x+r)}{\Gamma(r) x !}(1-p)^{r} p^{x} \\ &=\frac{(x+r-1) !}{(r-1) ! x !} p^{x}(1-p)^{r} \\ &=N B(r, p) \end{aligned}$$

这样的分布其实已经可以满足scHiC数据的离散特性和过度分散性。但是，实际的scHiC数据还具有稀疏性，因此在NB的基础上，进一步的发展出ZINB，即零膨胀负二项分布。

• 零膨胀负二项分布
  定义一个示性函数$I_0(x)$: $$I_0(x) = \left\{ \begin{aligned} 1 & & x = 0 \\ 0 & & x = 1 \end{aligned} \right.$$ 零膨胀负二项分布的概率密度函数为： $$f_{Z I N B}(m \mid \theta, r, p)=\theta \cdot I_{0}(m)+(1-\theta) \cdot f_{N B}(m \mid r, p)$$

式中，$\theta$可以认为是真实的基因表达值被观测为0的概率。

reference:

单细胞RNA-seq数据分布的选择
单细胞数据分析工具scvi介绍