位运算
位运算是一种计算机对于二进制数据的运算。
位运算的几种运算符
位运算的几种运算符:下边写的很多二进制数处于方便都只写了一个字节,8位,因为大多数运算的举例都是按照正数举例的,所以对运算结果没什么影响,但实际上,int类型在c++中占四个字节,32位。
- $\And$: 与运算,当两位都为1时,运算的结果为1,否则为0。 例: $3 \And 5$,计算机在计算时先将其转化为二进制,即$0000 \; 0011 \And 0000 \; 0101$,与运算的结果就是二进制数对于每一位相与后的结果,即$0000 \; 0001$,转化为十进制就是$1$。
- $ | $ :或运算,当两位同时为0时,结果为0,否则运算的结果为1。 同样的例子: $3 \; | \; 5$,还是先将十进制转换为二进制,在每一位上做或运算。最后得到的结果是$0000 \; 0111$,转化为十进制就是$7$。
- ^ :异或运算,当两位相同时,结果为0,否则结果为1。例: $3 \; $ ^ $ \; 5$,转化为二进制后,异或运算的结果是$0000 \; 0110$,转化为十进制就是$6$。
- ~:取反运算,将二进制数的每一位取反。例: $~3$,转化为二进制后,取反运算的结果是$1111 \; 1100$,转化为十进制就是$-4$。
- ‘<<’:左移,将二进位全部左移若干位,高位丢弃,低位补0。例: $3 \; << \; 2$,转化为二进制后,左移两位的结果是$0000 \; 1100$,转化为十进制就是$12$。
- ‘>>’: 右移,将二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移)。例: $3 \; >> \; 2$,转化为二进制后,右移两位的结果是$0000 \; 0000$,转化为十进制就是$0$。而对于负数来说,就根据编译器的不同有所不同了,在c++中,右移是以补码形式参与运算,正数左右移、负数左移均以补 0 操作(符号位保持不变),负数右移以补 1 操作(符号位不变)。对于$-3 \; >> \; 2$,先取-3的补码,即$1111 \; 1111 \; 1111 \; 1111 \; 1111 \; 1111 \; 1111\; 1101$,算数右移两位直接在补码的前边补1,运算的的结果是$1111 \; 1111$(中间省略掉了很多组1),由补码转换为原码,即$1000 \; 0001$,转化为十进制就是$-1$。逻辑补码则是在补码的前边补0,运算的结果是$0011 \; 1111$(中间同样省略掉了很多组1),转化为十进制就是$1073741823$,就是2。
/*在c++中,逻辑右移和算数右移公用一个运算符,>>,由编译器决定使用逻辑右移还是算术右移,当运
算数的类型为unsigned时,使用逻辑右移,当运算数的类型为signed时,使用算数右移。*/
# include <iostream>
# include <bitset>
using namespace std;
int main() {
int a = -0b11;
int logit = (unsigned)a >> 2;
int cal = a >> 2;
cout << bitset<sizeof(a) * 8>(a) << endl;
cout << a << endl;
cout << bitset<sizeof(logit) * 8>(logit) << endl; // 逻辑右移
cout << bitset<sizeof(cal) * 8>(cal) << endl; // 算数右移
cout << logit << endl;
cout << cal << endl;
return 0;
}
/*
out: 11111111111111111111111111111101
-3
00111111111111111111111111111111
11111111111111111111111111111111
1073741823
-1
*/bit_xor,bit_or和bit_and
bit_xor,bit_or和bit_and是c++20的新特性,作用是对两个数组进行迭代的异或,或和与运算,并返回结果,与transform函数结合返回一个新的数组,新数组的每个元素是对应元素的异或,或和与运算结果。用法如下:
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
using namespace std;
int main() {
vector<int> a = { 1, 2, 3, 4, 5 };
vector<int> b = { 1, 1, 3, 4, 5 };
vector<int> c(a.size());
transform(a.begin(), a.end(), b.begin(), c.begin(), bit_xor<int>());
for (auto i : c) {
cout << i << " ";
}
cout << endl;
return 0;
}
/* out: 0 1 0 0 0 */bit_and和bit_or的用法相同:
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
using namespace std;
int main() {
vector<int> a = { 1, 2, 3, 4, 5 };
vector<int> b = { 1, 1, 3, 4, 5 };
vector<int> c(a.size());
transform(a.begin(), a.end(), b.begin(), c.begin(), bit_and<int>());
for (auto i : c) {
cout << i << " ";
}
cout << endl;
return 0;
}
/* out: 1 0 3 4 5 */bit_xor同样也可以与accumulate函数结合,统计数组中出现次数为奇数次的元素,用法如下:
# include <iostream>
# include <vector>
# include <algorithm>
# include <functional>
# include <numeric>
using namespace std;
int main() {
vector<int> a = { 1, 2, 2, 1, 5 };
int res = accumulate(a.begin(), a.end(), 0, bit_xor<int>());
cout << res << endl;
return 0;
}
/* out: 5 */上边的这段代码等价于:
# include <iostream>
# include <vector>
using namespace std;
int main() {
vector<int> a = { 1, 2, 2, 1, 5 };
int res = 0;
for (auto i : a) {
res ^= i;
}
cout << res << endl;
return 0;
}这样,我们就可以秒了leetcode的136题只出现一次的数字
这道题一眼看上去可以用哈希表来做:
class Solution {
public:
int singleNumber(vector<int>& nums) {
unordered_map<int, int> mp;
for(auto p : nums) {
auto iter = mp.find(p);
if(iter == mp.end()) {
mp[p] = 1;
}
else {
iter->second += 1;
}
}
for(auto p : mp) {
if(p.second == 1) {
return p.first;
}
}
return -1;
}
};但是哈希表额外的占用了$O(n)$的空间,如果使用位运算,我们可以这样做:
class Solution {
public:
int singleNumber(vector<int>& nums) {
return accumulate(nums.begin(), nums.end(), 0, bit_xor());
}
};这样,时间复杂度为$O(n)$,而且不用使用额外的空间。
另一道可以使用位运算解决的题目是二进制中1的个数。
这道题第一眼看上去的话,思路就是把二进制数转化为字符串,然后遍历字符串去找到其中1的个数。但是,一个实际的问题是,to_string()存入字符串的是十进制的数字。而这样做显然也不够优雅,背离了题目的本意。因此,考虑使用位运算的方法来解决。
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while(n != 0) {
res++;
n = n & (n - 1);
}
return res;
}
};这种做法是比较容易想到的做法,每次将n减1与n相与,都可以消去最右边的1,这样循环直至将n变为0,就可以得到1的个数。这种做法的时间复杂度是$O(1)$,因为最多循环32次。
第k个语法符号也是一道需要使用位运算来解决的题目。
这道题可以看作是一个完全二叉树的构造:
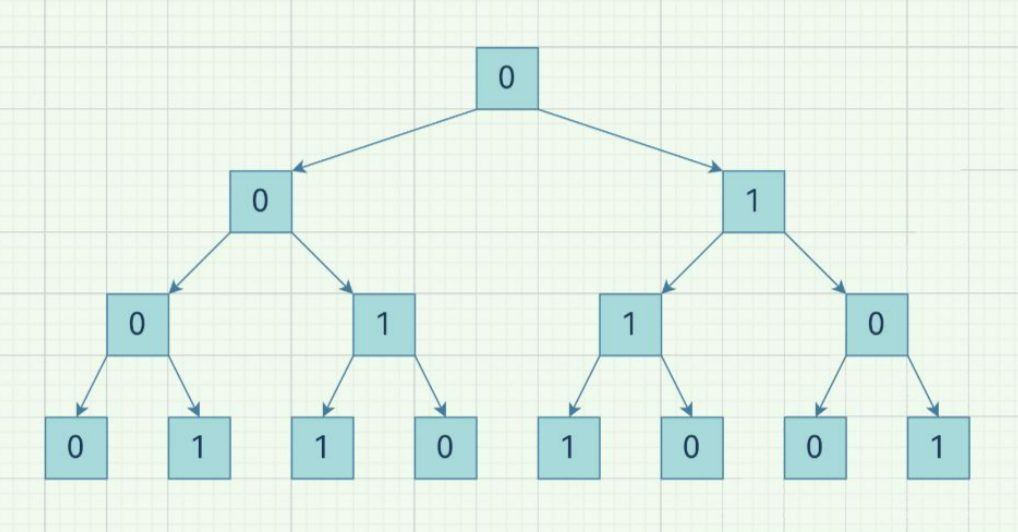
从图中,我们可以看出,一个节点的值取决于它的父节点的值,而当这个节点为父节点的左子节点时,它的值与父节点的值相同,当这个节点为父节点的右子节点时,它的值与父节点的值相异。这样我们只需要判断这个节点是左子节点还是右子节点,以及它的父节点的值即可。因此,我们可以使用递归的方法来解决这道题。
class Solution {
public:
int kthGrammar(int n, int k) {
if(n == 1) {
return 0;
}
if(k % 2 == 0) { // 右子节点
return kthGrammar(n - 1, k / 2) == 0 ? 1 : 0;
}
else { // 左子节点
return kthGrammar(n - 1, (k + 1) / 2) == 0 ? 0 : 1;
}
}
};
使用位运算可以简化这个代码,kthGrammar(n - 1, (k + 1) / 2) == 0 ? 0 : 1这个三元运算符可以直接使用异或运算来代替。简化后的代码如下。
class Solution {
public:
int kthGrammar(int n, int k) {
if(n == 1) {
return 0;
}
return (!(k % 2)) ^ kthGrammar(n - 1, (k + 1) / 2);
}
};正则表达式
正则表达式是另一种奇技淫巧,用来检查一个串中是否含有某种子串,将匹配的子串替换或从某个串中取出符合要求的子串。
怎么去写一个正则表达式
基本语法:
[ABC]表示匹配[ABC]中的所有字符。[^ABC]表示匹配除了[ABC]之外的所有字符。[A-Z]表示匹配一个区间,匹配所有的大写字母。.表示匹配除了换行符之外的所有字符。[\s\S]表示匹配所有的字符。其中,[\s]表示匹配所有空白符,包括换行,[\S]表示匹配所有非空白符,不包括换行。[\w]表示匹配所有的字母,数字和下划线。
特殊字符
*表示匹配前面的字符0次或多次。+表示匹配前面的字符1次或多次。?表示匹配前边的字符0次或1次。|指明两项之间的一个选择,例如a|b表示匹配a或b。$表示匹配输入字符串的结尾位置。()表示一个子表达式的开始和结束位置。\转义字符,在表示特殊字符时统统要使用转义字符加以修饰。
量词
*表示匹配前面的字符0次或多次。+表示匹配前面的字符1次或多次。?表示匹配前边的字符0次或1次。{n}表示匹配前面的字符n次。{n,}表示匹配前面的字符至少n次。{n,m}表示匹配前面的字符至少n次,至多m次。
正则表达式在python的基本用法
python中提供了使用正则表达式的re模块。
re.match()函数:尝试从字符串的起始位置匹配一个模式,如果不是起始位置匹配成功的话,match()就返回none。若匹配成功,返回模式所占的区间。re.match(pattern, string, flags = 0) # pattern: 匹配的正则表达式 # string: 要匹配的字符串re.search()函数:扫描整个字符串并返回第一个成功的匹配。re.search(pattern, string, flags = 0) # pattern: 匹配的正则表达式 # string: 要匹配的字符串re.sub()函数:替换字符串中的匹配项。re.sub(pattern, repl, string, count = 0, flags = 0) # repl: 替换的字符串 # count: 模式匹配后的最大替换次数,默认0表示替换所有的匹配 # 返回替换后的字符串re.compile()函数:用于编译正则表达式生成一个正则表达式的对象,供match()和search()这两个函数使用。re.compile(pattern, flags = 0) # pattern: 正则表达式的字符串或原生字符串表示 # flags: 可选,表示匹配模式上文所述的
flags的具体参数如下:re.I忽略大小写re.M多行模式re.S即为.并且包括换行符在内的任意字符(.不包括换行符)re.L表示特殊字符集\w, \W, \b, \B, \s, \S依赖于当前环境re.U表示特殊字符集\w, \W, \b, \B, \d, \D, \s, \S依赖于Unicode字符属性数据库re.X为了增加可读性,忽略空格和#后面的注释
突然发现正则表达式这个坑比我想象的要大上不少,先干活,接下来有时间再慢慢看。

