刷题到现在,稍微有了一点点手感,所以从今天开始,重点要刷一刷剑指offer了。这里将记录在刷剑指offer的过程中,一些自己的题解。
1 - 5
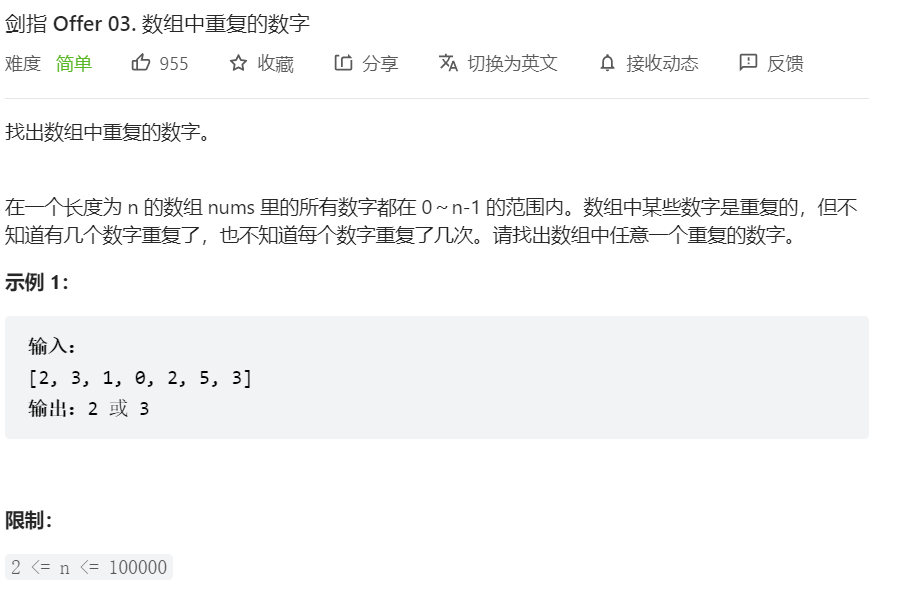
- 题解:
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
unordered_map<int, int> mp;
for(auto p : nums) {
auto iter = mp.find(p);
if(iter != mp.end()) {
return p;
}
mp[p] = 1;
}
return -1;
}
};没什么好说的,直接构建哈希表就可以秒了。
但是思考一下是不是还有更节省空间开销的方法呢。是有的。直接在原地对数组进行修改,因为数组中的数字一定在$(0, n-1)$范围内,所以,可以用数组中数字的下标进行映射,这样就节省了构建哈希表所需的空间开销。
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
// 时间复杂度On,空间复杂度On
for(int i = 0; i < nums.size(); i++) {
while(nums[i] != i) {
if(nums[i] == nums[nums[i]]) {
return nums[i];
}
swap(nums[i], nums[nums[i]]);
}
}
return 0;
}
};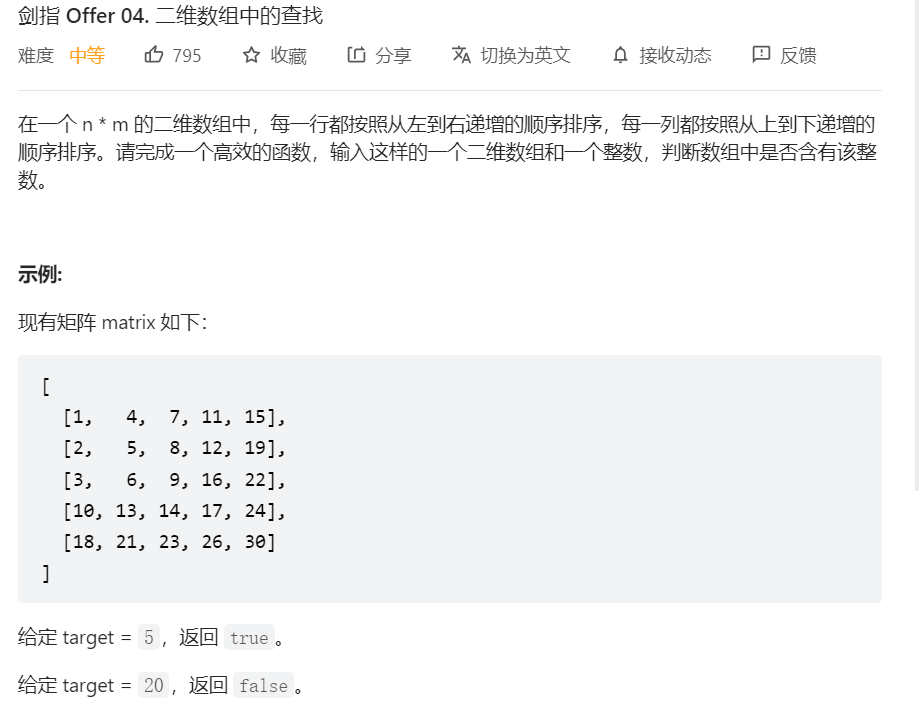
- 题解:
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if(matrix.size() == 0 || matrix[0].size() == 0) {
return false;
}
for(auto p : matrix) {
// 确定在这个区间中进行二分查找
if(p[0] <= target && p.back() >= target) {
int left = 0, right = p.size() - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(p[mid] == target) {
return true;
}
else if(p[mid] > target) {
right = mid - 1;
}
else if(p[mid] < target) {
left = mid + 1;
}
}
}
}
return false;
}
};这题主要考的是二分法,从头遍历二维数组的行,每次判断一下要找的数是否就在这一行。确定行之后用二分查找就行。这里的二分,是要查找是否值存在,对于找左边界,右边界,和值是否存在,二分都有不同的写法,如下所示。
// 坚持左闭右开
int binary_search(vector<int> nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
}
else if(nums[mid] > target) {
right = mid;
}
else if(nums[mid] < target) {
left = mid + 1;
}
}
return -1;
}
int left_bound(vector<int> nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
right = mid;
}
else if(nums[mid] > target) {
right = mid;
}
else if(nums[mid] < target) {
left = mid + 1;
}
}
return left;
}
int right_bound(vector<int> nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
left = mid + 1;
}
else if(nums[mid] > target) {
right = mid;
}
else if(nums[mid] < target) {
left = mid + 1;
}
}
return right - 1;
// 这里返回 right - 1 是因为左闭右开
} 实现左右边界的查找,区别只在于,找到一个跟目标值相等的值之后,是要将区间向左收缩还是向右收缩,若是寻找右边界,就向右收缩,改变left的值,若是寻找左边界,就向左收缩,改变right的值。
二分查找还有一种类型,就是找到数组中距目标值最近的那个下标。
int nearest(vector<int> nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
}
else if(nums[mid] > target) {
right = mid;
}
else if(nums[mid] < target) {
left = mid + 1;
}
}
if(left == 0) {
return left;
}
if(left == nums.size()) {
return left - 1;
}
return abs(nums[left] - target) < abs(nums[left - 1] - target) ? left : left - 1;
}其实还是原汁原味的二分查找,只是在最后返回的时候,如果没有找到target,返回我们最终收缩到的那个区间即可。
class Solution {
public:
string replaceSpace(string s) {
string res;
for(auto p : s) {
if(p == ' ') {
res += "%20";
}
else {
res += p;
}
}
return res;
}
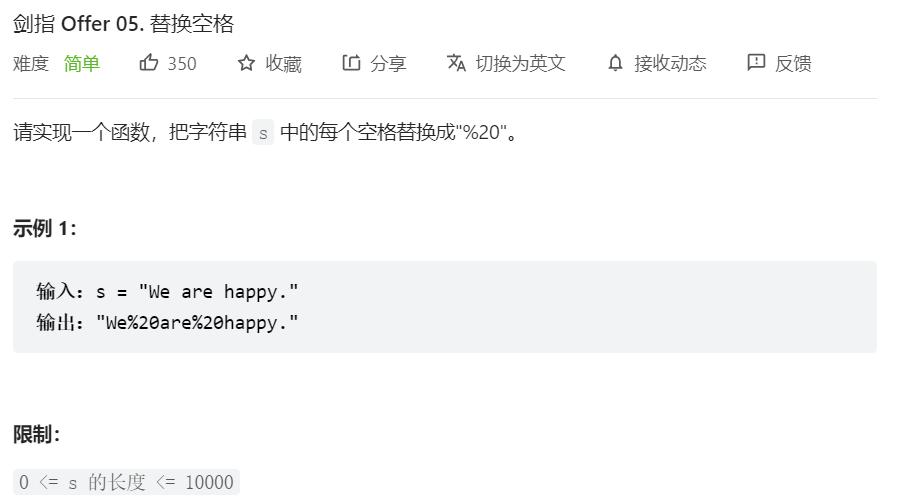
};首先想到的不容易翻车的解决方案是用一个新的字符串,遍历老字符串,不是空格就复制,如果检测到空格则在新字符串加入”%20”。这样的时间复杂度为$O(n)$,空间复杂度是$O(n)$。为了节省空间复杂度,想一下原地修改的方案,借鉴自代码随想录。
class Solution {
public:
string replaceSpace(string s) {
// 在原字符串上进行修改,从后往前修改
int count = 0;
int o_size = s.size();
for(auto p : s) {
if(p == ' ') {
count += 1;
}
}
// 扩充原字符串的空间
s.resize(s.size() + count * 2);
int n_size = s.size();
for(int i = o_size - 1, j = n_size - 1; i < j; j--, i--) {
if(s[i] != ' ') {
s[j] = s[i];
}
else {
s[j] = '0';
s[j - 1] = '2';
s[j - 2] = '%';
j -= 2;
}
}
return s;
}
};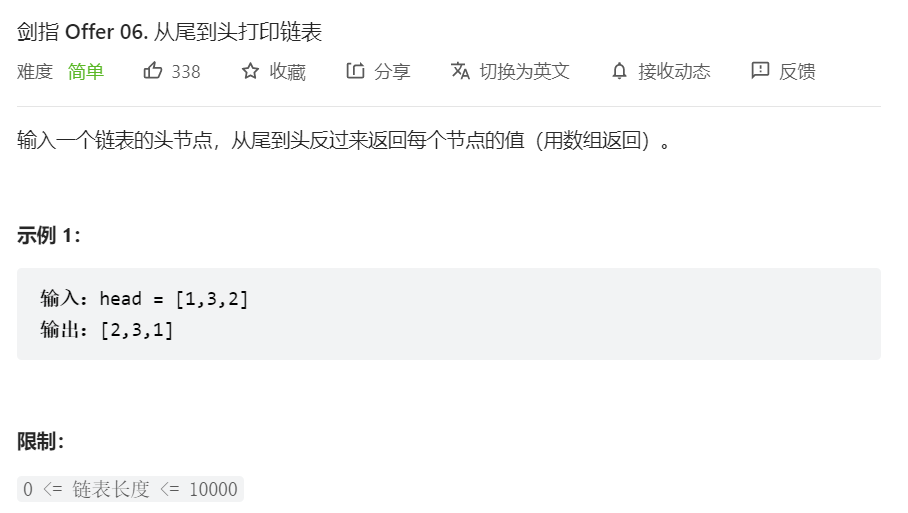
- 题解
class Solution {
public:
vector<int> res;
vector<int> reversePrint(ListNode* head) {
// if(head == nullptr) return {};
// stack<ListNode*> s;
// vector<int> res;
// while(head != nullptr) {
// s.push(head);
// head = head->next;
// }
// while(!s.empty()) {
// auto node = s.top();
// s.pop();
// res.push_back(node->val);
// }
// return res;
// 递归 后序遍历
if(head == nullptr) return res;
reversePrint(head->next);
res.push_back(head->val);
return res;
}
};常规思路,栈或者递归。没什么好说的。
- 题解
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size() == 0 || inorder.size() == 0) return nullptr;
// 找到根节点
TreeNode* root = new TreeNode(*preorder.begin());
// 利用中序数组找到左子树和右子树,指针以左是左子树,右是右子树
auto iter = find(inorder.begin(), inorder.end(), root->val);
vector<int> iLeft(inorder.begin(), iter);
vector<int> iRight(iter + 1, inorder.end());
// 划分前序数组
int n = iLeft.size();
vector<int> pLeft(preorder.begin() + 1, preorder.begin() + 1 + n);
vector<int> pRight(preorder.begin() + 1 + n, preorder.end());
// 递归重建左子树和右子树
root->left = buildTree(pLeft, iLeft);
root->right = buildTree(pRight, iRight);
return root;
}
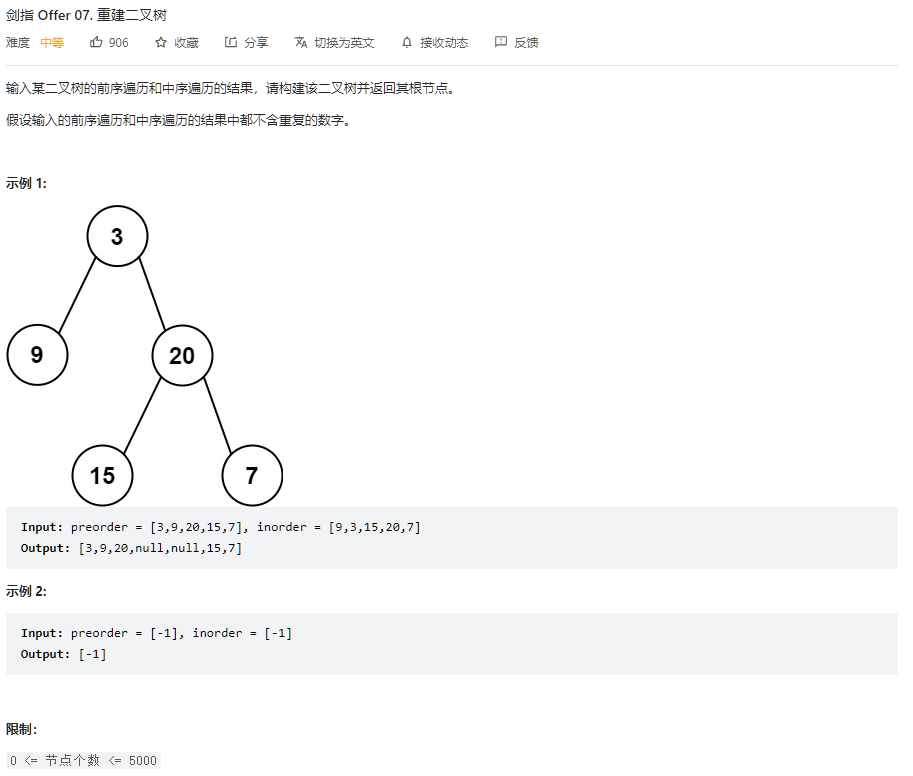
};这题确实是把我难到了。。。复习一下前序遍历和中序遍历的顺序,前序遍历是根左右,中序遍历是左右根。主要是通过前序遍历找到当前的根节点,然后再通过中序遍历划分出左子树和右子树,再用划分出的左子树和右子树的大小在前序遍历的数组中划分出左子树和右子树,最后递归的解决问题。
6 - 10
- 题解
class CQueue {
private:
stack<int> in, out;
void in2out() {
while(!in.empty()) {
out.push(in.top());
in.pop();
}
}
public:
CQueue() {
}
void appendTail(int value) {
in.push(value);
}
int deleteHead() {
if(out.empty()) {
if(in.empty()) {
return -1;
}
in2out();
}
int value = out.top();
out.pop();
return value;
}
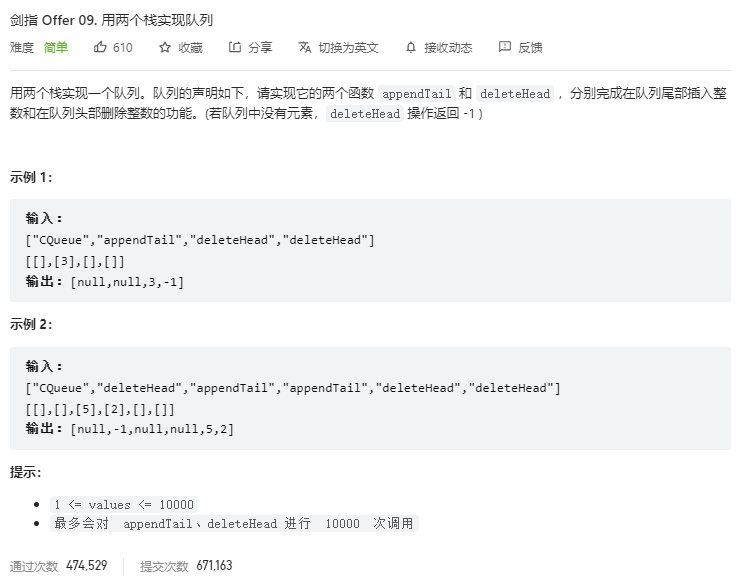
};ez题,重要的是快速读题。这题的意思是用两个栈实现队列,队列是先进先出,栈是先进后出,所以我们可以用一个栈来存储数据,另一个栈来输出数据,当输出栈为空时,将输入栈的数据全部倒入输出栈,这样输出栈的数据就是先进先出的顺序了。
- 题解
class Solution {
public:
int fib(int n) {
if(n == 0) return 0;
else if(n == 1) return 1;
auto res = fib(n - 1) + fib(n - 2);
return res % 1000000007;
}
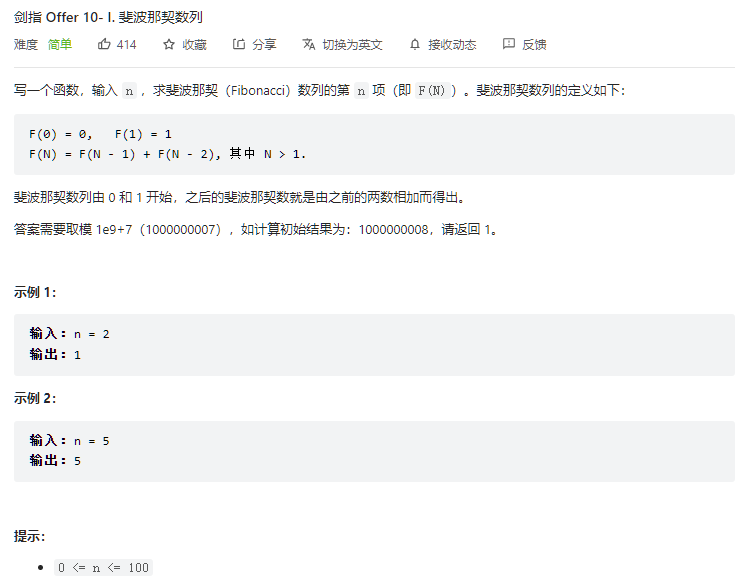
};陈年老题了,直接递归,好吧,吃了个tl。
正经的用dp做一下,时间复杂度为$O(n)$,空间复杂度为$O(1)$。
class Solution {
public:
int fib(int n) {
if(n == 0) return 0;
else if(n == 1) return 1;
int pre = 0, cur = 1;
for(int i = 2; i <= n; i++) {
int temp = cur;
cur = (cur + pre) % 1000000007;
pre = temp;
}
return cur;
}
};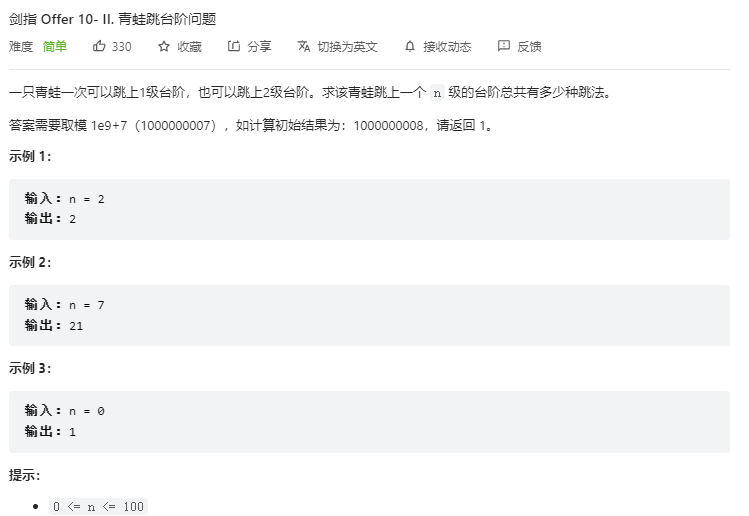
- 题解
class Solution {
public:
int numWays(int n) {
if(n == 0) return 1;
else if(n > 0 && n <= 2) return n;
int pre = 1, cur = 2;
for(int i = 3; i <= n; i++) {
int temp = cur;
cur = (pre + cur) % 1000000007;
pre = temp;
}
return cur;
}
};11 - 15
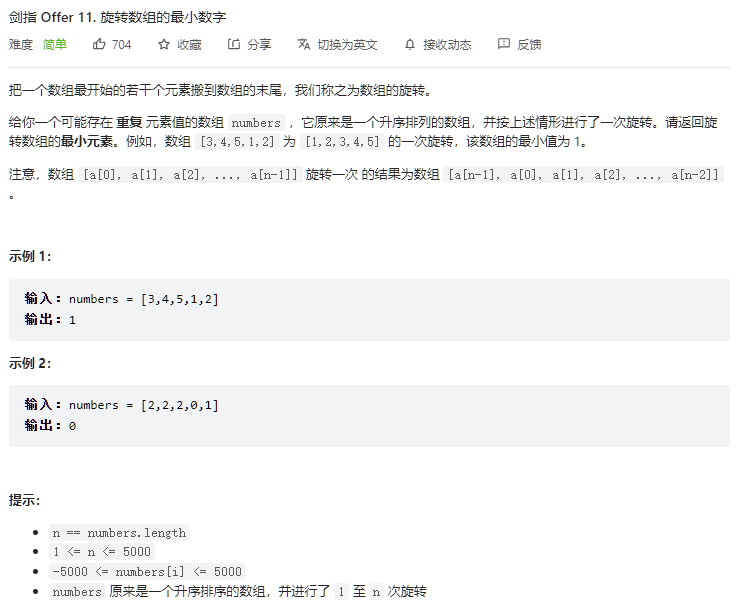
- 题解
class Solution {
public:
int minArray(vector<int>& numbers) {
for(int i = 1; i < numbers.size(); i++) {
if(numbers[i] < numbers[i-1]) {
return numbers[i];
}
}
return numbers[0];
}
};看评论区说,似乎还可以用二分法。
class Solution {
public:
int minArray(vector<int>& numbers) {
int left = 0, right = numbers.size() - 1;
while(left < right) {
int mid = left + (right - left) / 2;
if(numbers[mid] < numbers[right]) {
right = mid;
}
else if(numbers[mid] > numbers[right]) {
left = mid + 1;
}
else {
right--;
}
}
return numbers[right];
}
};这里用二分法主要是为了表示自己知道可以利用部分有序的特性降低时间复杂度,好吧,面向面试编程和面向ac编程。

- 题解
class Solution {
public:
vector<vector<int>> used;
bool check(int i, int j, int k, vector<vector<char>>& board, string word) {
if(board[i][j] != word[k]) return false;
else if(k == word.length() - 1) return true;
used[i][j] = true;
vector<pair<int, int>> directions = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
bool result = false;
for(auto &p : directions) {
if(i + p.first >= 0 && i + p.first < board.size() && j + p.second >= 0 && j + p.second < board[0].size()) {
if(!used[i + p.first][j + p.second]) {
bool flag = check(i + p.first, j + p.second, k + 1, board, word);
if(flag) {
result = true;
break;
}
}
}
}
used[i][j] = false;
return result;
}
bool exist(vector<vector<char>>& board, string word) {
used = vector<vector<int>> (board.size(), vector<int> (board[0].size(), false));
for(int i = 0; i < board.size(); i++) {
for(int j = 0; j < board[0].size(); j++) {
bool flag = check(i, j, 0, board, word);
if(flag) {
return true;
}
}
}
return false;
}
};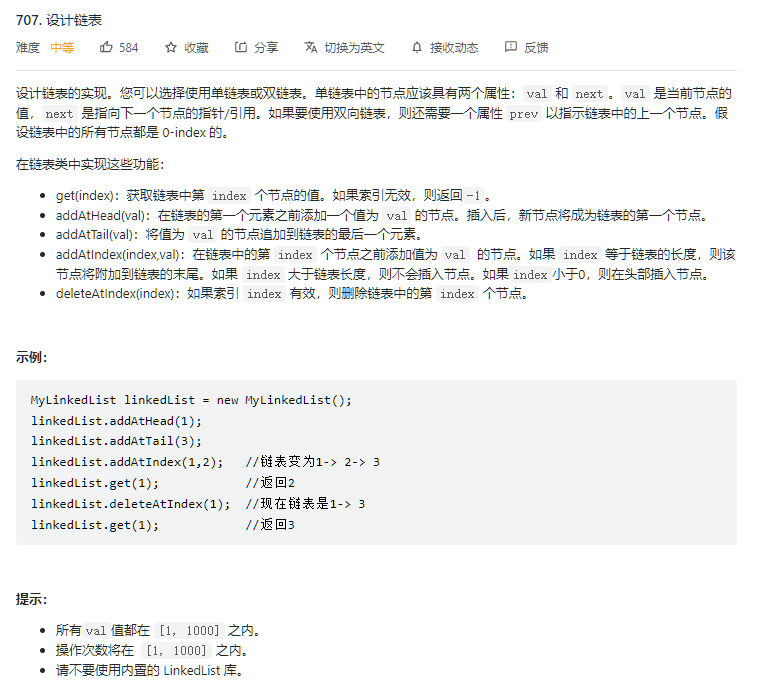
- 题解
class MyLinkedList {
public:
struct _ListNode{
int val;
_ListNode* next;
_ListNode() : val(0), next(nullptr) {};
_ListNode(int val) : val(val), next(nullptr) {};
_ListNode(int val, _ListNode* next) : val(val), next(next) {};
};
_ListNode* _dummy;
int _size;
MyLinkedList() {
_dummy = new _ListNode(-1);
_size = 0;
}
int get(int index) {
if(index >= _size) return -1;
auto cur = _dummy->next;
while(index--) {
cur = cur->next;
}
return cur->val;
}
void addAtHead(int val) {
auto o_head = _dummy->next;
_dummy->next = new _ListNode(val);
_dummy->next->next = o_head;
_size++;
}
void addAtTail(int val) {
auto cur = _dummy;
while(cur->next) {
cur = cur->next;
}
cur->next = new _ListNode(val);
_size++;
}
void addAtIndex(int index, int val) {
if(index > _size) return;
auto cur = _dummy;
while(index--) {
cur = cur->next;
}
auto buffer = cur->next;
cur->next = new _ListNode(val);
cur->next->next = buffer;
_size++;
}
void deleteAtIndex(int index) {
if(index >= _size) return;
auto cur = _dummy;
while(index--) {
cur = cur->next;
}
cur->next = cur->next->next;
_size--;
}
};插播一道每日一题设计链表,我觉得这个题还是很有意思的,每当自信满满提交的时候总会因为各种想不到的边界条件吃一发wa。
再插播一道不同的二叉搜索树,这道题既有树又有回溯,第一时间没什么思路。
- T95 .不同的二叉搜索树2
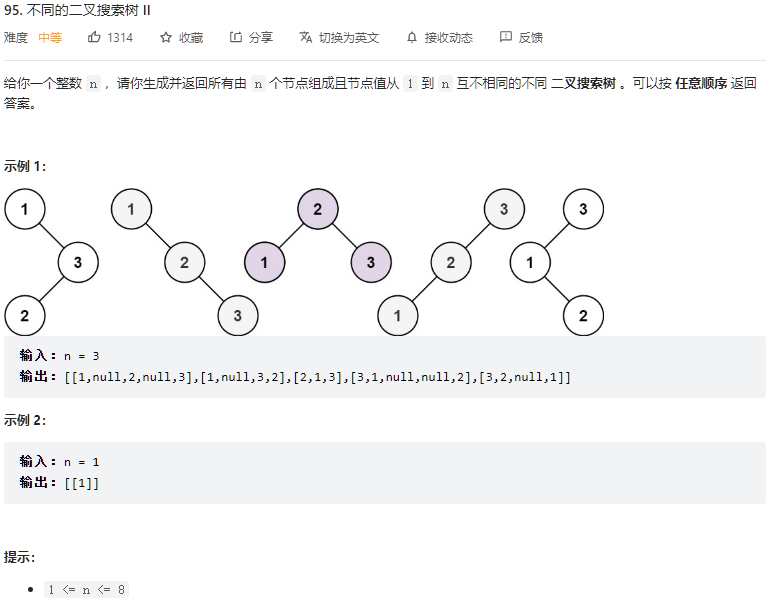
- 题解
class Solution {
public:
vector<TreeNode*> backtrack(int start, int end) {
if(start > end) return { nullptr };
vector<TreeNode*> allTrees;
for(int i = start; i <= end; i++) {
// 获取所有的左子树
vector<TreeNode*> left_trees = backtrack(start, i - 1);
// 获取所有的右子树
vector<TreeNode*> right_trees = backtrack(i + 1, end);
// 拼接
for(auto left : left_trees) {
for(auto right : right_trees) {
TreeNode* root = new TreeNode(i);
root->left = left;
root->right = right;
allTrees.push_back(root);
}
}
}
return allTrees;
}
vector<TreeNode*> generateTrees(int n) {
return backtrack(1, n);
}
};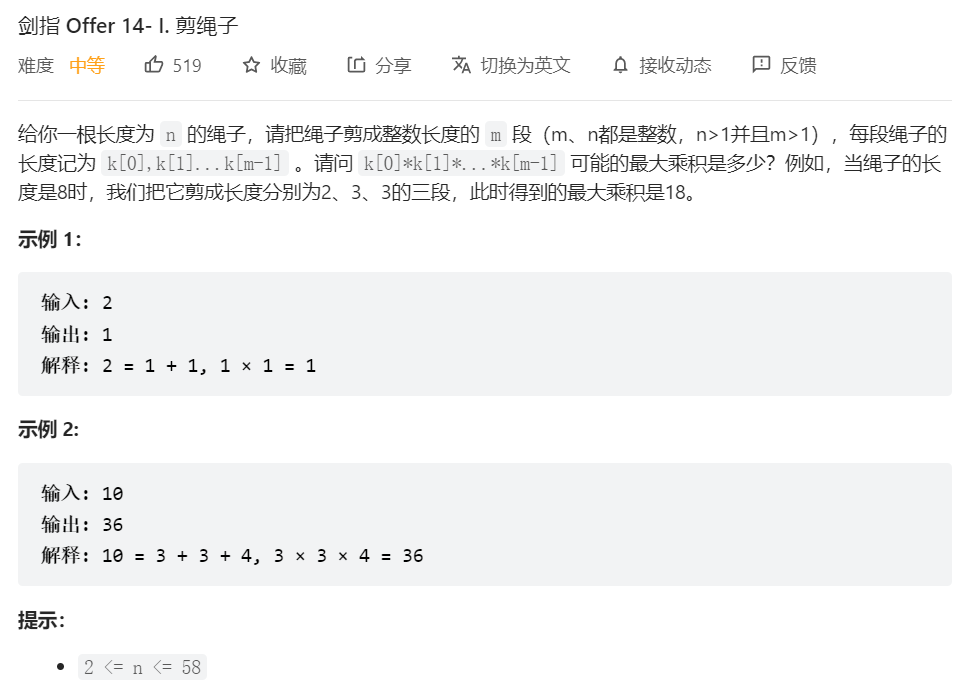
找规律题,最优的拆分方案一定是尽可能多的拆出3来。
- 题解
class Solution {
public:
int cuttingRope(int n) {
if(n == 2) return 1;
if(n == 3) return 2;
//尽可能多的将拆成3
int m = n % 3;
if(m == 1) {
if(n > 4) {
return 4 * pow(3, (n - 4) / 3);
}
else {
return 4;
}
}
else if(m == 2) {
return 2 * pow(3, (n - 2) / 3);
}
else {
return pow(3, n / 3);
}
}
};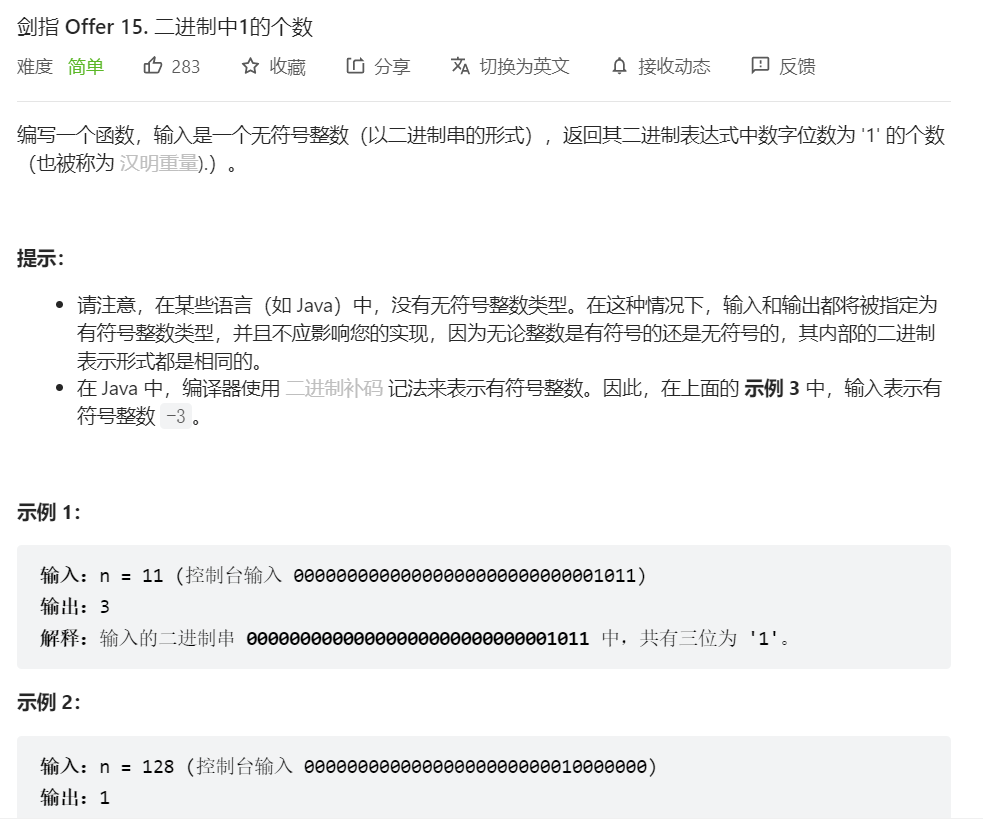
使用位运算。每次将n减1与n相与,都可以消去最右边的1,这样循环直至将n变为0,就可以得到1的个数。这种做法的时间复杂度是$O(1)$,因为最多循环32次
- 题解
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while(n != 0) {
res++;
n = n & (n - 1);
}
return res;
}
};16 - 20

- 题解
最容易想到的那一定是:
class Solution {
public:
double myPow(double x, int n) {
return pow(x, n);
}
};但是这样容易找不到工作。
class Solution {
public:
double quickPow(double x, int n) {
if(n == 0) {
return 1;
}
double y = quickPow(x, n / 2);
return n % 2 == 0 ? y * y : y * y * x;
}
double myPow(double x, int n) {
int N = abs(n);
return n > 0 ? quickPow(x, N) : 1 / quickPow(x, N);
}
};使用递归的思想可以减小一定的问题规模,快速幂在不考虑大数的情况下还是很好实现的。

- 题解
class Solution {
public:
vector<int> printNumbers(int n) {
vector<int> res;
int max_n = 0;
for(int i = 0; i < n; i++) {
max_n += 9 * pow(10, i);
}
// res.push_back(max_n);
for(int i = 0; i < max_n; i++) {
res.push_back(i + 1);
}
return res;
}
};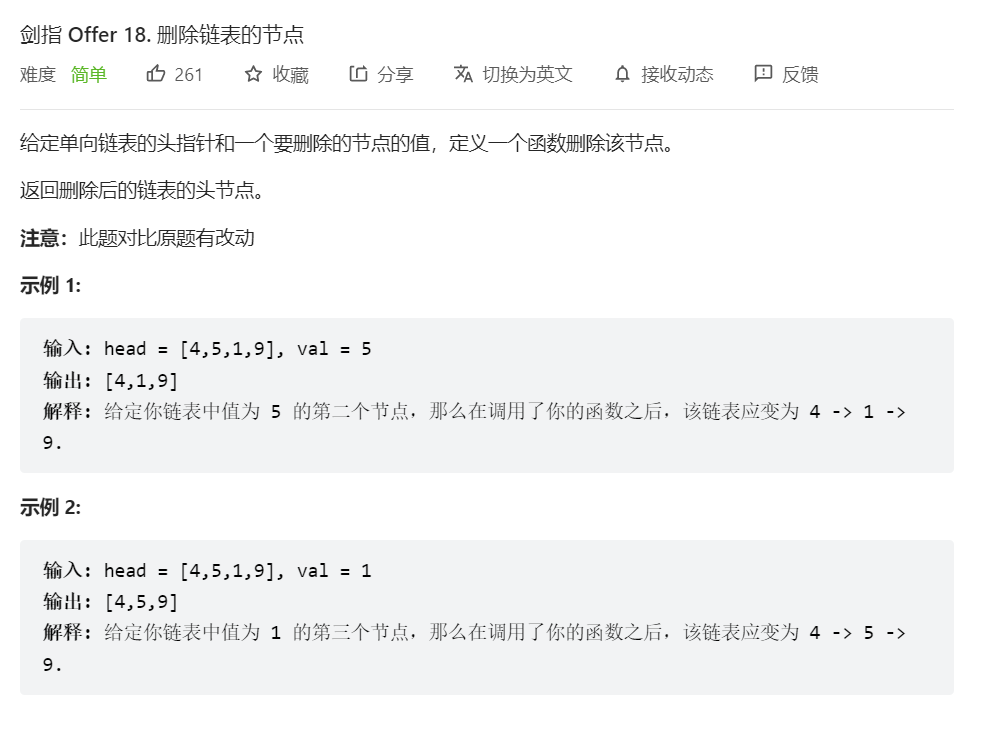
- 题解
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
ListNode* dummy = new ListNode(-1);
dummy->next = head;
auto cur = head;
auto pre = dummy;
while(cur) {
if(cur->val == val) {
pre->next = cur->next;
return dummy->next;
}
else {
pre = cur;
cur = cur->next;
}
}
return dummy->next;
}
};21 - 25
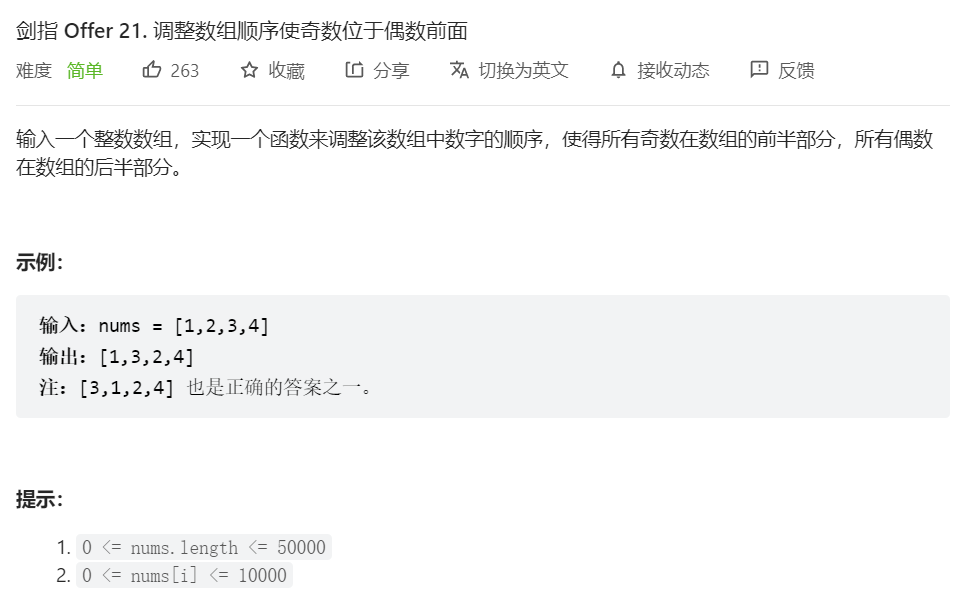
- 题解
可以使用双数组,也可以使用双指针。
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
// 双数组
// vector<int> even;
// vector<int> odd;
// for(int i = 0; i < nums.size(); i++) {
// if(nums[i] % 2 == 0) {
// even.push_back(nums[i]);
// }
// else {
// odd.push_back(nums[i]);
// }
// }
// for(int i = 0; i < even.size(); i++) {
// odd.push_back(even[i]);
// }
// return odd;
// 双指针
int left = 0, right = 0;
while(right < nums.size()) {
if(nums[right] % 2 == 0) {
right++;
}
else {
swap(nums[left], nums[right]);
left++;
right++;
}
}
return nums;
}
};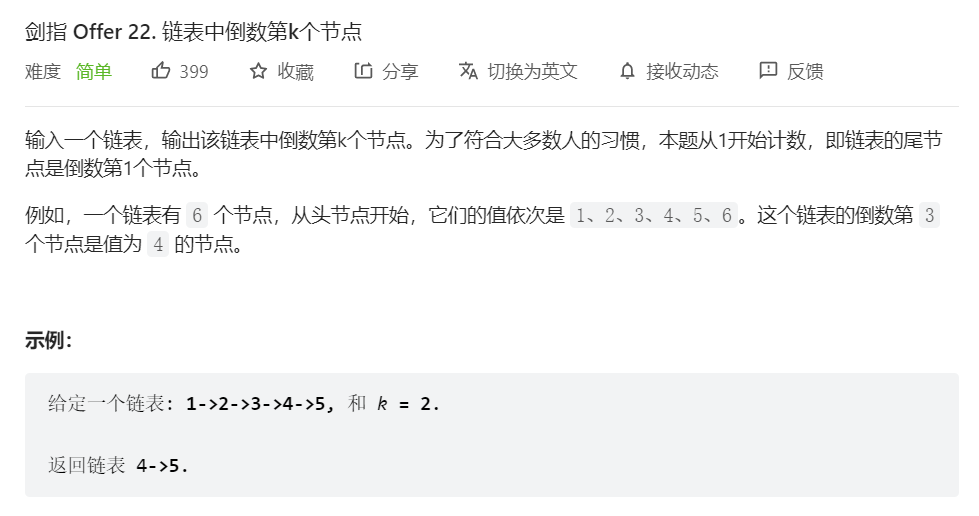
- 题解
双指针的经典应用——快慢指针。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
auto left = head;
auto right = head;
for(int i = 0; i < k; i++) {
right = right->next;
}
while(right) {
left = left->next;
right = right->next;
}
return left;
}
};
- 题解
栈的方式太常规,而且要使用额外的存储空间,这里就不再赘述。写一种遍历的方式。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
auto cur = head;
while(cur) {
auto buffer = cur->next;
cur->next = pre;
pre = cur;
cur = buffer;
}
return pre;
}
};
- 题解
同样是经典的双指针问题。好多链表题都可以用双指针来做。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode(-1);
auto cur = dummy;
// 双指针
while(l1 || l2) {
if(l1 == nullptr && l2) {
cur->next = l2;
return dummy->next;
}
if(l1 && l2 == nullptr) {
cur->next = l1;
return dummy->next;
}
if(l1->val <= l2->val) {
cur->next = l1;
l1 = l1->next;
}
else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
return dummy->next;
}
};26 - 30

- 题解
整体逻辑就是,先判断A和B的根节点是否相同,若不同,则判断B是否是A的左子树或者右子树的子结构,若相同,则判断B的左子树和右子树是否和A的左子树和右子树相同,若不同,则继续判断B是否是A的左子树或者右子树的子结构。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool dfs(TreeNode* A, TreeNode* B) {
if(B == nullptr) {
return true;
}
if(A == nullptr) {
return false;
}
return A->val == B->val && dfs(A->left, B->left) && dfs(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if(A == nullptr || B == nullptr) {
return false;
}
return dfs(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
};
- 题解
前序遍历,交换左右子树即可。
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
traverse(root);
return root;
}
void traverse(TreeNode* root) {
if(root == nullptr) return;
swap(root->right, root->left);
traverse(root->left);
traverse(root->right);
}
};
- 题解
class Solution {
public:
bool dfs(TreeNode* l, TreeNode* r) {
if(l == nullptr && r == nullptr) {
return true;
}
if(l == nullptr || r == nullptr) {
return false;
}
return l->val == r->val && dfs(l->left, r->right) && dfs(l->right, r->left);
}
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return true;
return dfs(root->left, root->right);
}
};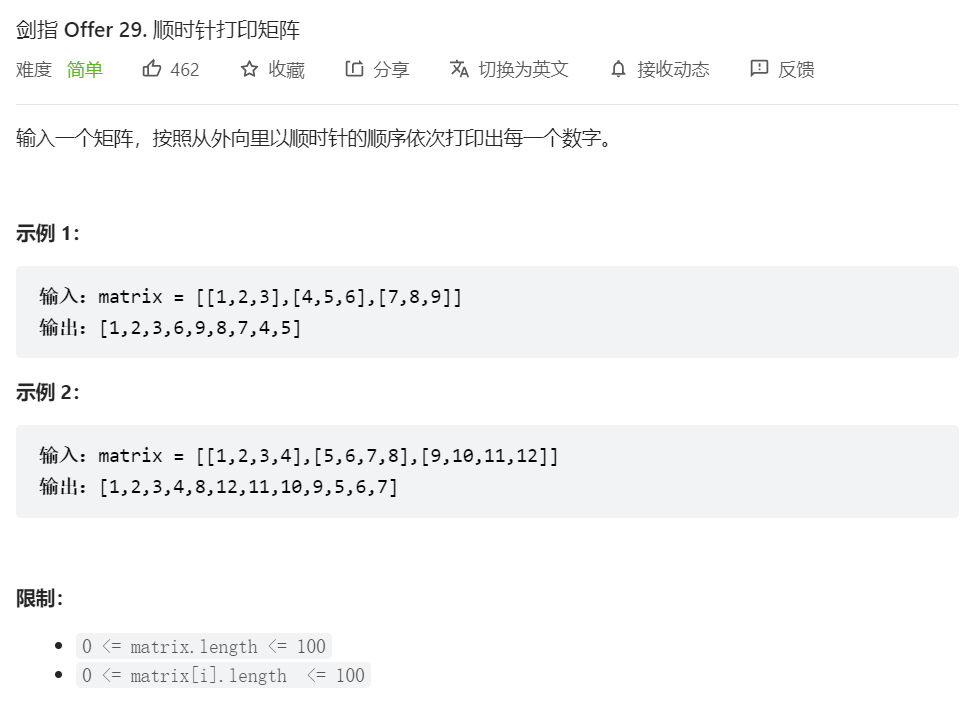
- 题解
主站的mid,到剑指就成easy了。模拟,主要是划定边界,每次走完一条边之后都要收缩边界,同时判断是否会越界。若越界,则退出循环。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
// 检查边界,每走一次,将相对应的边界向内缩
vector<int> res;
if(matrix.size() == 0) return res;
int top = 0;
int bottom = matrix.size() - 1;
int left = 0;
int right = matrix[0].size() - 1;
while(1) {
for(int i = left; i <= right; i++) {
res.push_back(matrix[top][i]);
}
if(++top > bottom) break;
for(int i = top; i <= bottom; i++) {
res.push_back(matrix[i][right]);
}
if(--right < left) break;
for(int i = right; i >= left; i--) {
res.push_back(matrix[bottom][i]);
}
if(--bottom < top) break;
for(int i = bottom; i >= top; i--) {
res.push_back(matrix[i][left]);
}
if(++left > right) break;
}
return res;
}
};
设计类的题目,这题如果可以使用标准库的stack的话将十分简单,每次push之前,将之前的最小值放进去,pop的时候也一起pop,这样就可以保证每次min的时候都是$O(1)$的时间复杂度。
class MinStack {
private:
stack<int> elements;
int min_element = INT_MAX;
public:
/** initialize your data structure here. */
MinStack() {
}
void push(int x) {
elements.push(min_element);
min_element = min_element > x ? x : min_element;
elements.push(x);
}
void pop() {
elements.pop();
min_element = elements.top();
elements.pop();
}
int top() {
return elements.top();
}
int min() {
return min_element;
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->min();
*/但是显然我们在面试的时候不应该向面试官展示强大的api调用能力。所以我们尝试用链表实现。
class MinStack {
private:
struct _ListNode {
int val;
int min;
_ListNode* next;
_ListNode(int x, int m) : val(x), min(m), next(nullptr) {}
};
_ListNode* _dummy;
int _size;
public:
/** initialize your data structure here. */
MinStack() {
_dummy = new _ListNode(0, INT_MAX);
_size = 0;
}
void push(int x) {
auto cur = _dummy;
while(cur->next) {
cur = cur->next;
}
cur->next = new _ListNode(x, min(cur->min, x));
_size++;
}
void pop() {
auto cur = _dummy;
while(cur->next->next) {
cur = cur->next;
}
cur->next = nullptr;
_size--;
}
int top() {
auto cur = _dummy;
while(cur->next) {
cur = cur->next;
}
return cur->val;
}
int min() {
auto cur = _dummy;
while(cur->next) {
cur = cur->next;
}
return cur->min;
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->min();
*/自定义一个链表节点的结构体,每个节点中储存当前节点的值和当前节点之前的最小值,保证min的时间复杂度为$O(1)$。
31 - 35
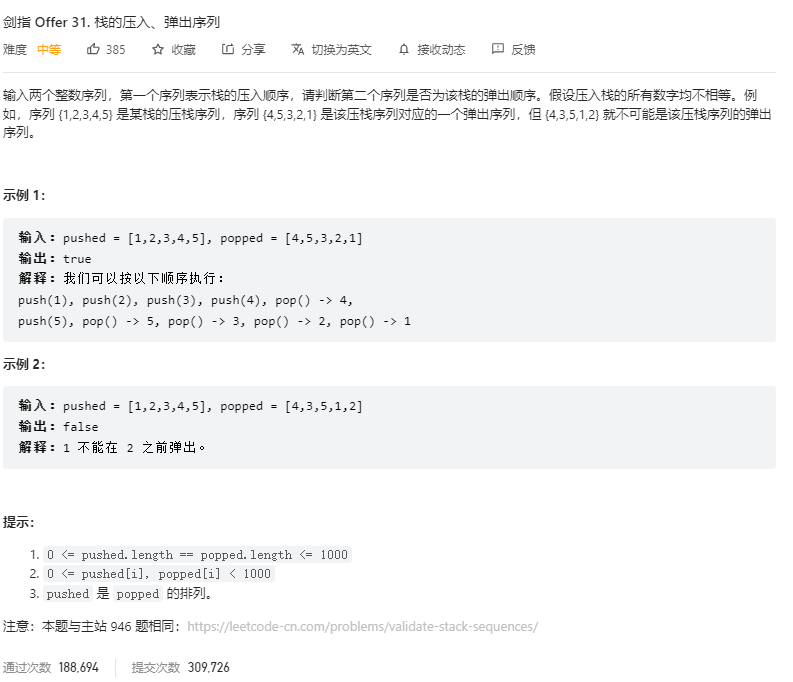
这道题目的思路很简单,简单的模拟一下就好。我们维护一个栈,每次将pushed中的元素压入栈中,然后判断栈顶元素是否等于popped中的元素,如果相等则弹出,否则继续压入,直到pushed中的元素全部压入栈中,然后判断栈是否为空即可。
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> s;
int i = 0;
for(auto p : pushed) {
s.push(p);
while(!s.empty() && s.top() == popped[i]) {
s.pop();
i++;
}
}
return s.size() == 0;
}
};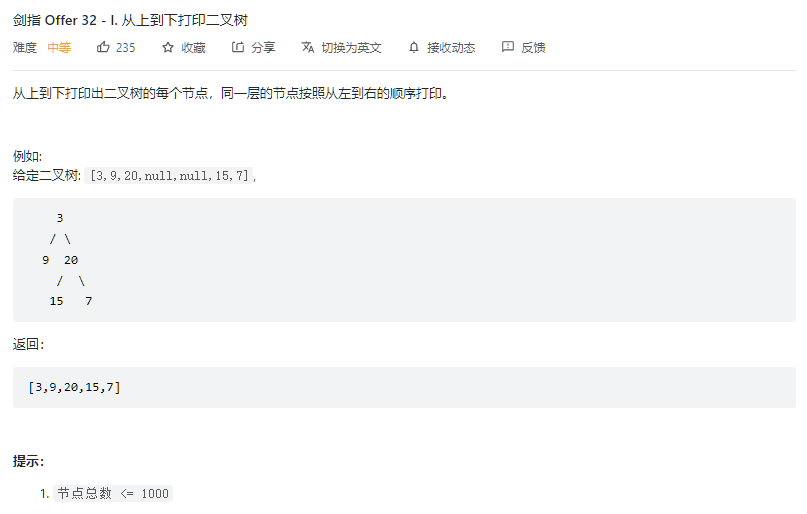
不懂为啥这题是个中等。
简单的层序遍历。
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
// 层序遍历
if(root == nullptr) return {};
queue<TreeNode*> q;
q.push(root);
vector<int> res;
while(!q.empty()) {
auto cur = q.front();
if(cur->left) q.push(cur->left);
if(cur->right) q.push(cur->right);
res.push_back(cur->val);
q.pop();
}
return res;
}
};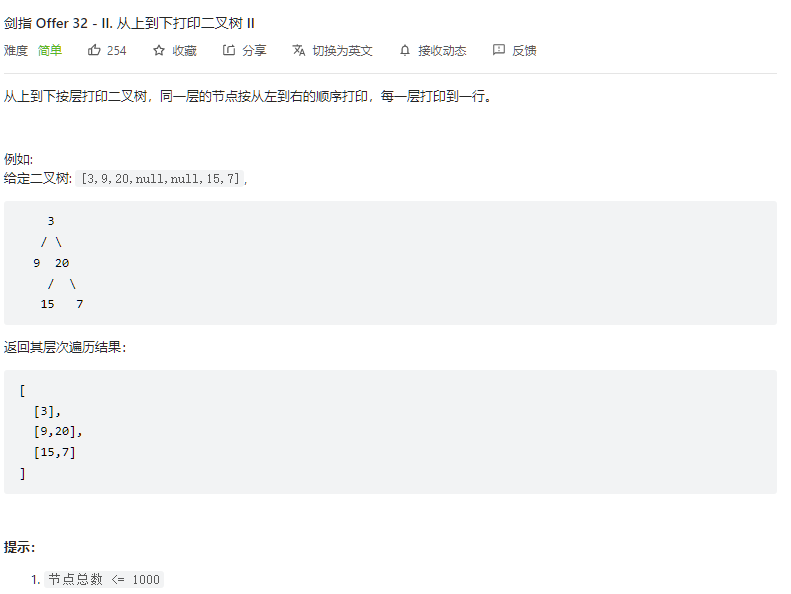
跟上一道题差不多吧。只是在最后返回的时候把每一层的结果放到一个vector中。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(root == nullptr) return {};
queue<TreeNode*> q;
q.push(root);
vector<vector<int>> res;
while(!q.empty()) {
int sz = q.size();
vector<int> buffer;
for(int i = 0; i < sz; i++) {
auto cur = q.front();
if(cur->left) q.push(cur->left);
if(cur->right) q.push(cur->right);
buffer.push_back(cur->val);
q.pop();
}
res.push_back(buffer);
}
return res;
}
};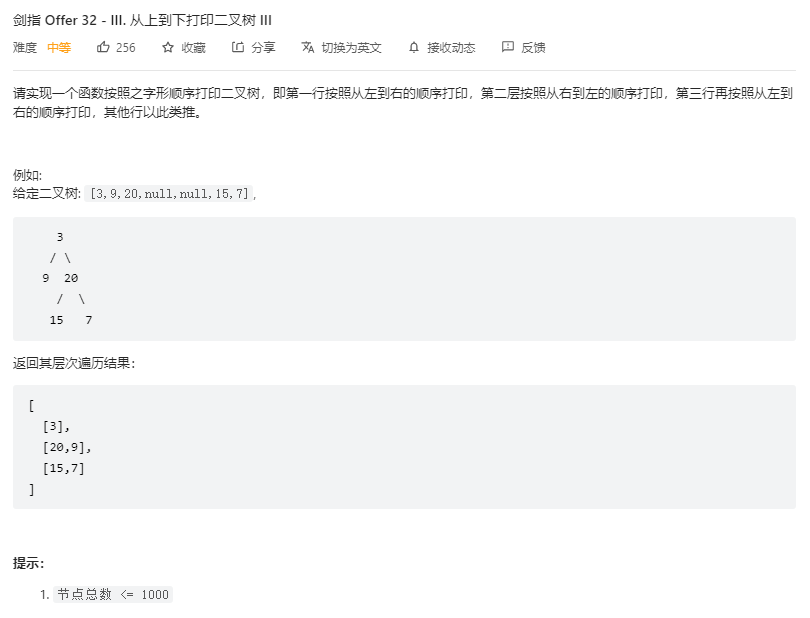
还是上道题的升级版,把原来的queue换成deque,然后每次处理一层时判断一下是奇数层还是偶数层就好。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(root == nullptr) return {};
deque<TreeNode*> q;
q.push_back(root);
vector<vector<int>> res;
while(!q.empty()) {
int sz = q.size();
vector<int> buffer;
for(int i = 0; i < sz; i++) {
TreeNode* cur;
if((res.size() % 2) == 0) {
cur = q.front();
if(cur->left) q.push_back(cur->left);
if(cur->right) q.push_back(cur->right);
buffer.push_back(cur->val);
q.pop_front();
}
else {
cur = q.back();
if(cur->right) q.push_front(cur->right);
if(cur->left) q.push_front(cur->left);
buffer.push_back(cur->val);
q.pop_back();
}
}
res.push_back(buffer);
}
return res;
}
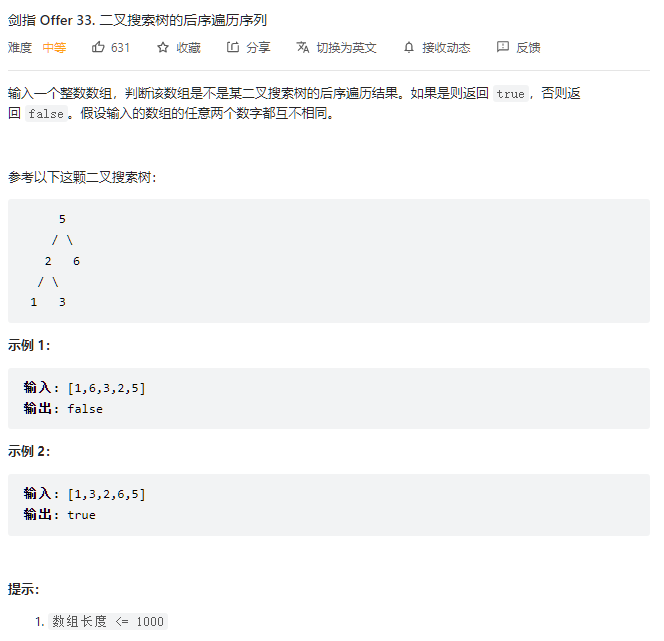
};- 剑指offer33.二叉搜索树的后序遍历序列
class Solution {
public:
bool help(vector<int> nums, int i, int j) {
if (i >= j) return true;
int p = i;
while (nums[p] < nums[j]) p++;
int m = p;
while (nums[p] > nums[j]) p++;
return p == j && help(nums, i, m - 1) && help(nums, m, j - 1);
}
bool verifyPostorder(vector<int>& postorder) {
return help(postorder, 0, postorder.size() - 1);
}
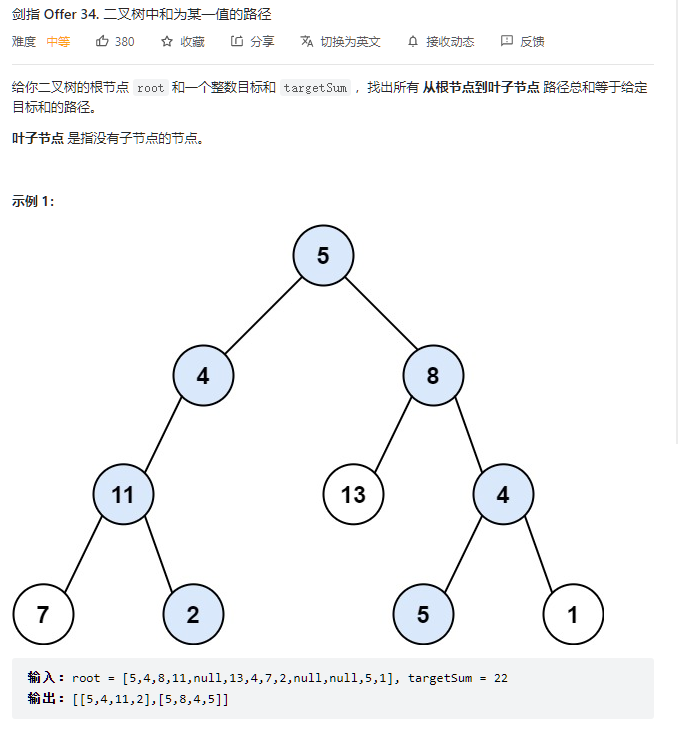
};- 剑指offer34.二叉树中和为某一值的路径
class Solution {
public:
vector<vector<int>> res;
void dfs(TreeNode* root, int target, vector<int> path) {
if(root == nullptr) {
return;
}
path.push_back(root->val);
if(root->left == nullptr && root->right == nullptr && target - root->val == 0) {
res.push_back(path);
return;
}
if(root->left) dfs(root->left, target - root->val, path);
if(root->right) dfs(root->right, target - root->val, path);
}
vector<vector<int>> pathSum(TreeNode* root, int target) {
vector<int> path;
dfs(root, target, path);
return res;
}
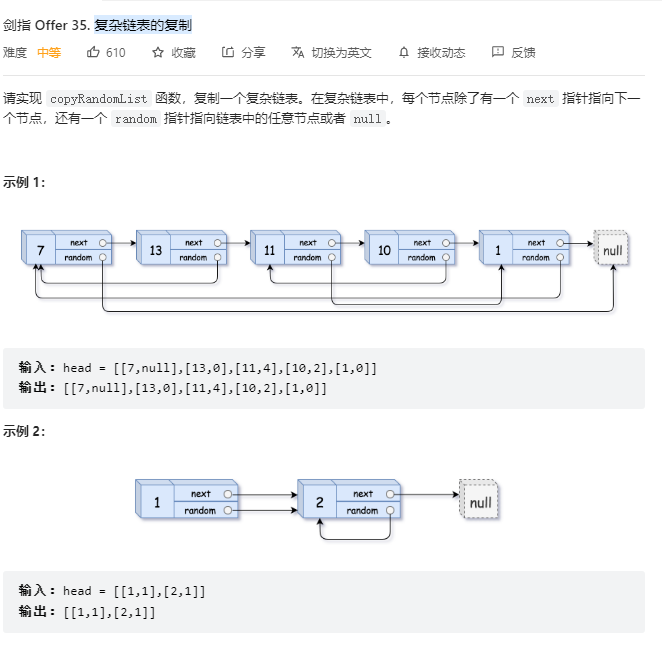
};- 剑指offer35.复杂链表的复制
class Solution {
public:
Node* copyRandomList(Node* head) {
if(head == nullptr) return nullptr;
Node* dummy = new Node(-1);
Node* cur = dummy;
Node* pre = head;
while(pre) {
Node* buffer = new Node(pre->val);
cur->next = pre;
pre = pre->next;
cur->next->next = buffer;
cur = cur->next->next;
}
cur = dummy->next;
while(cur) {
if(cur->random != nullptr) {
cur->next->random = cur->random->next;
}
cur = cur->next->next;
}
// 错误的思路 修改了原链表
// cur = dummy->next->next;
// while(cur) {
// if(cur->next) {
// cur->next = cur->next->next;
// }
// else {
// break;
// }
// cur = cur->next;
// }
// 正确的做法是,在两个链表拆开时,同时也要把原链表归位
Node* node1 = dummy->next;
Node* ans = dummy->next->next;
Node* node2 = ans;
while(node1) {
Node* buffer = node2->next != nullptr ? node2->next->next : nullptr;
node1->next = node1->next->next;
node2->next = buffer;
node1 = node1->next;
node2 = node2->next;
}
return ans;
}
};
