bfs

leetcode
刷题赎罪
发布日期:   2022-09-06
更新日期:   2022-09-22
文章字数:   2.4k
阅读次数:  

BFS

BFS即广度优先搜索，是一种图论算法，用于在图中寻找两个节点之间的最短路径。它的基本思想是，从起始节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。如果目标节点被发现，则算法中止。广度优先搜索是一种盲目搜索，它并不试图找到最优解，而是以较低的代价找到可行解。广度优先搜索算法的时间复杂度为O(V+E)，其中V是顶点的数量，E是边的数量。

BFS的框架

int step = 0;
void bfs(Node* root, Node* target) {
    queue<Node*> q;
    set<Node*> visited;
    q.push(root); // 将起始节点加入队列
    while (!q.empty()) {
        int size = q.size();
        for (int i = 0; i < size; i++) {
            Node* cur = q.front();
            q.pop();
            // 判断是否到达终点
            if (cur == target) {
                return;
            }
            if (visited.find(cur) != visited.end()) // 如果已经访问过，跳过
                continue;
            visited.insert(cur);
            // 将cur的相邻节点加入队列
            for (Node* next : cur->neighbors) {
                q.push(next);
            }
        }
        step++; // 增加步数
    }
}

若bfs的对象为二叉树，仅有父节点指向子节点的指针而没有子节点指向父节点的指针时，不需要担心会走回头路的问题，可以不需要visited数组。若有子节点指向父节点的指针，则需要visited数组来记录已经访问过的节点，避免走回头路。

BFS的应用

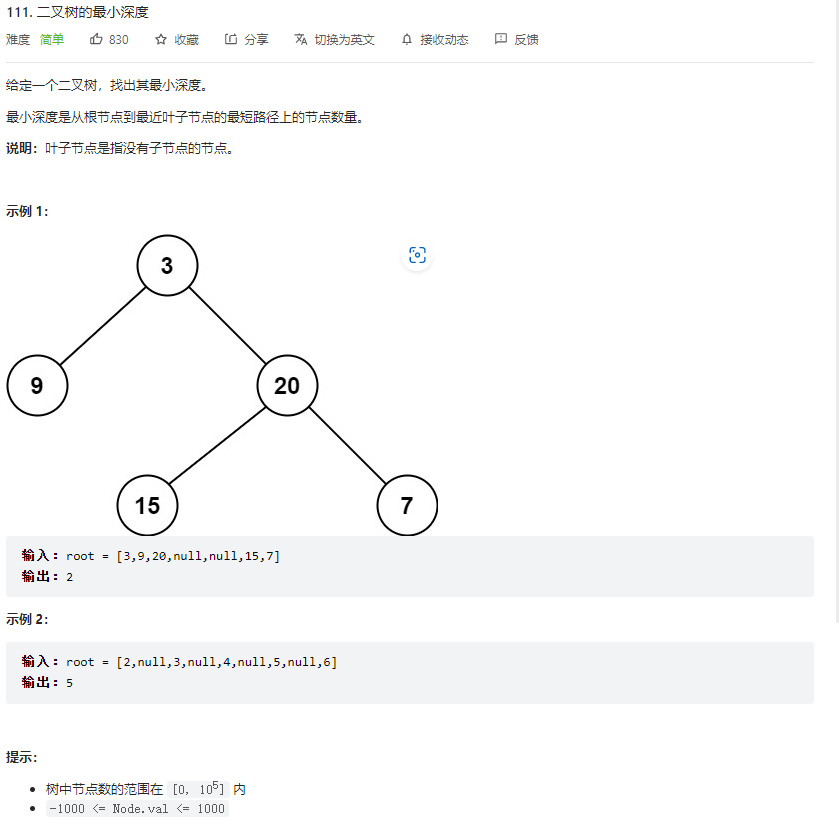
111. 二叉树的最小深度

题解：

class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        int res = 1;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()) {
            int sz = q.size();
            for(int i = 0; i < sz; i++) {
                TreeNode* cur = q.front();
                q.pop();
                if(cur->left == nullptr && cur->right == nullptr) {
                    return res;
                }
                if(cur->left) {
                    q.push(cur->left);
                }
                if(cur->right) {
                    q.push(cur->right);
                }
            }
            res++;
        }
        return res;
    }
};

这道题的题解完全套用上文的bfs框架，只需要设置合理的终止条件：当遍历到的节点的左右子节点都为空时，返回当前的步数。（同时由于你扣的优秀测例还需要考虑根节点为空的情况。。。）

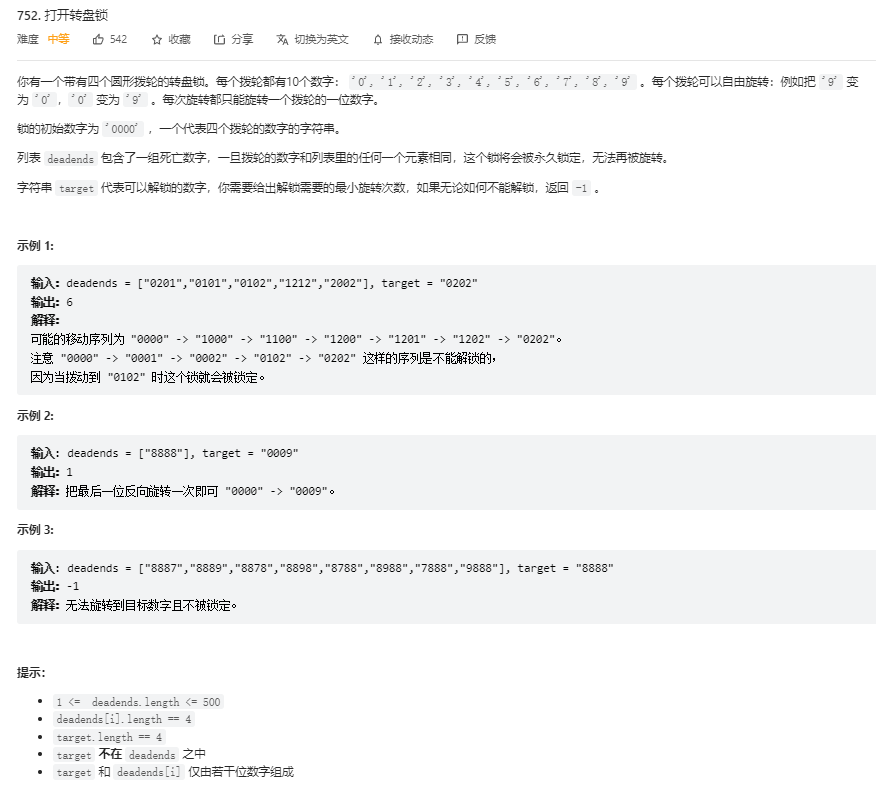
752. 打开转盘锁

题解：

class Solution {
public:
    string up(string s, int p) {
        if(s[p] == '9') s[p] = '0';
        else s[p] += 1; 
        return s;
    }
    string down(string s, int p){
        if(s[p] == '0') s[p] = '9';
        else s[p] -= 1; 
        return s;
    }
    int openLock(vector<string>& deadends, string target) {
        unordered_set<string> us;
        for(auto p : deadends) {
            if(p == "0000") {
                return -1;
            }
            us.emplace(p);
        }
        int res = 0;
        queue<string> q;
        unordered_set<string> visited;
        q.push("0000");
        visited.emplace("0000");
        while(!q.empty()) {
            int sz = q.size();
            for(int i = 0; i < sz; i++) {
                string cur = q.front();
                q.pop();
                // 判断是否到达终点
                if(cur == target) {
                    return res;
                }
                // 将相邻节点加入队列,若相邻节点是死结点或者已经遍历过的节点则不加入
                for(int j = 0; j < 4; j++) {
                    string u = up(cur, j);
                    string d = down(cur, j);
                    if(us.find(u) == us.end() && visited.find(u) == visited.end()) {
                        q.push(u);
                        visited.emplace(u);
                    }
                    
                    if(us.find(d) == us.end() && visited.find(d) == visited.end()) {
                        q.push(d);
                        visited.emplace(d);
                    }
                }
            }
            res += 1;
        }
        return -1;
    }
};

这题的题解也是完全套用上文的bfs框架，字符串的变化相当于字符串的相邻节点，需要注意在保证相邻节点不是已经遍历过的之外还需要保证相邻节点不是死结点。（再吐槽一次你扣的优秀测例”0000”放在deadends里边）
使用vector find和unordered_set find效率完全不同，使用vector find时直接测例超时不能通过，unordered_set的查找效率更高，因此使用unordered_set来存储死结点和访问过的节点。

这道题还可以使用双向bfs来优化，参考这里。bfs的时间复杂度常常与图的边和节点数有关，而图的边和节点在一定情况下可能出现指数级的扩大，因此使用双向bfs可以大幅度的减少时间复杂度。这里给出一个c++的双向bfs的模板：

int step = 0;
void bfs(Node* root, Node* target) {
    queue<Node*> q1;
    queue<Node*> q2;
    unordered_set<Node*> visited;

    q1.push(root); // 将起始节点加入队列1
    q2.push(target); // 将终止节点加入队列2

    while (!q1.empty() && !q2.empty()) {
        // 从节点数较少的队列开始遍历,尽可能的降低复杂度
        if (q1.size() > q2.size()) {
            swap(q1, q2);
        }
        int sz = q1.size();
        for (int i = 0; i < sz; i++) {
            Node* cur = q1.front();
            q1.pop();
            // 判断是否到达终点
            if (q2.find(cur) != q2.end()) {
                return step;
            }
            for (auto p : cur->next) {
                if (visited.find(p) == visited.end()) {
                    q1.push(p);
                    visited.emplace(p);
                }
            }
        }
        step += 1;
    }
}

对于这道题，也可以使用双向bfs来优化：

class Solution {
public:
    string up(string s, int p) {
        if(s[p] == '9') s[p] = '0';
        else s[p] += 1; 
        return s;
    }
    string down(string s, int p){
        if(s[p] == '0') s[p] = '9';
        else s[p] -= 1; 
        return s;
    }
    int openLock(vector<string>& deadends, string target) {
        unordered_set<string> us;
        for(auto p : deadends) {
            if(p == "0000") {
                return -1;
            }
            us.emplace(p);
        }
        int res = 0;
        unordered_set<string> q1;
        unordered_set<string> q2;
        unordered_set<string> visited;
        q1.emplace("0000");
        q2.emplace(target);
        visited.emplace("0000");
        while(!q1.empty() && !q2.empty()) {
            unordered_set<string> temp;
            if(q1.size() > q2.size()) {
                swap(q1, q2);
            }
            int sz = q1.size();
            for(auto cur : q1) {
                // 判断是否是死节点
                if(us.find(cur) != us.end()) {
                    continue;
                }
                visited.emplace(cur);
                // 判断是否到达终点
                if(q2.find(cur) != q2.end()) {
                    return res;
                }
                // 将相邻节点加入队列,若相邻节点已经遍历过的节点则不加入
                for(int j = 0; j < 4; j++) {
                    string u = up(cur, j);
                    string d = down(cur, j);
                    if(visited.find(u) == visited.end()) temp.emplace(u);
                    if(visited.find(d) == visited.end()) temp.emplace(d);
                }
            }
            q1 = q2;
            q2 = temp;
            res += 1;
        }
        return -1;
    }
};

运行结果如下所示，双向bfs的性能相对于单向bfs有了极大的提升。虽然本质上，传统的bfs和双向bfs的时间复杂度都是一样的，但是双向bfs往往可以增快算法运行的速度，因此在一些情况下，双向bfs是一个很好的选择。

运行结果

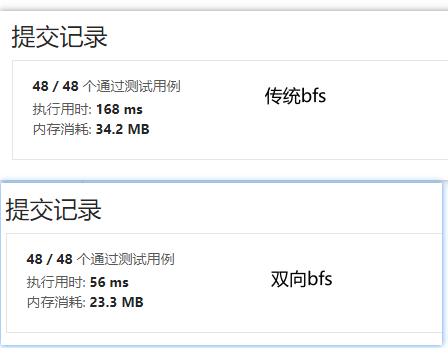
2022.9.21更新、

今天的每日一题是一道bfs，但是我发现我好像已经把bfs忘了，并不会做。。。再复习一下。

20220921152553

题解：

class Solution {
public:
    vector<string> find_neighbor(string s) {
        vector<string> res;
        for(int i = 0; i < s.size() - 1; i++) {
            for(int j = i + 1; j < s.size(); j++) {
                swap(s[i], s[j]);
                res.push_back(s);
                swap(s[i], s[j]);
            }
        }
        return res;
    }
    int kSimilarity(string s1, string s2) {
        // bfs
        queue<string> q;
        set<string> visited;
        q.push(s1);
        int step = 0;
        while(!q.empty()) {
            int sz = q.size();
            for(int i = 0; i < sz; i++) {
                auto cur = q.front();
                q.pop();
                // 是否到达终点
                if(cur == s2) {
                    return step;
                }
                // 是否曾经访问过
                if(visited.find(cur) != visited.end()) {
                    continue;
                }
                visited.emplace(cur);
                // 将所有邻居入队
                auto neighbors = find_neighbor(cur);
                for(auto p : neighbors) {
                    q.push(p);
                }
            }
            step++;
        }
        return -1;
    }
};

这道题直接使用上边的bfs框架显然是十分正确的。但是，时间复杂度太高了，单单是找邻居这一步就是$O(n^2)$的复杂度，别说个步骤在bfs中被反复的使用了。果不其然，提交了就是超时。

这样子超时之后最直观的想法就是优化一下找邻居这一步，所以，借鉴别人的思路，将find_neighbor这一步优化。

vector<string> find_neighbor(string s, string s2) {
    int i = 0;
    vector<string> res;
    while(s[i] == s2[i]) {
        i++;
    }
    for(int j = i + 1; j < s.size(); j++) {
        if(s[j] == s2[i] && s[j] != s2[j]) {
            swap(s[i], s[j]);
            res.push_back(s);
            swap(s[i], s[j]);
        }
    }
    return res;
}

这样就可以通过了。这里将找邻居的过程变成了一个贪心的过程，每次都找一个最起码向target靠近一位的邻居，这样就可以减少很多邻居的数量。但是不是很明白为什么这样可以找得到最优的结果。

优化后总体的代码如下：

class Solution {
public:
    vector<string> find_neighbor(string s, string s2) {
        int i = 0;
        vector<string> res;
        while(s[i] == s2[i]) {
            i++;
        }
        for(int j = i + 1; j < s.size(); j++) {
            if(s[j] == s2[i] && s[j] != s2[j]) {
                swap(s[i], s[j]);
                res.push_back(s);
                swap(s[i], s[j]);
            }
        }
        return res;
    }
    int kSimilarity(string s1, string s2) {
        // bfs 超时
        queue<string> q;
        set<string> visited;
        q.push(s1);
        int step = 0;
        while(!q.empty()) {
            int sz = q.size();
            for(int i = 0; i < sz; i++) {
                auto cur = q.front();
                q.pop();
                // 是否到达终点
                if(cur == s2) {
                    return step;
                }
                // 是否曾经访问过
                if(visited.find(cur) != visited.end()) {
                    continue;
                }
                visited.emplace(cur);
                // 将所有邻居入队
                auto neighbors = find_neighbor(cur, s2);
                for(auto p : neighbors) {
                    q.push(p);
                }
            }
            step++;
        }
        return -1;
    }
};

接下来尝试一些比较常规的想的明白的优化吧。比如上文说过的双向bfs。

class Solution {
public:
    vector<string> find_neighbor(string s) {
        vector<string> res;
        for(int i = 0; i < s.size() - 1; i++) {
            for(int j = i + 1; j < s.size(); j++) {
                swap(s[i], s[j]);
                res.push_back(s);
                swap(s[i], s[j]);
            }
        }
        return res;
    }
    int kSimilarity(string s1, string s2) {
        // 双向bfs
        int step = 0;

        set<string> q1;
        set<string> q2;
        set<string> visited;

        q1.emplace(s1);
        q2.emplace(s2);
        visited.emplace(s1);

        while(!q1.empty() && !q2.empty()) {
            set<string> temp;
            if(q1.size() > q2.size()) {
                swap(q1, q2);
            }
            // int sz = q1.size();
            for(auto cur : q1) {
                // 是否到达终点
                if(q2.find(cur) != q2.end()) {
                    return step;
                }
                visited.emplace(cur);
                // 邻居节点入队
                auto neighbors = find_neighbor(cur);
                for(auto p : neighbors) {
                    if(visited.find(p) != visited.end()) {
                        continue;
                    }
                    temp.emplace(p);
                }
            }
            q1 = q2;
            q2 = temp;
            step++;
        }
        return -1;
    }
};

好吧还是超时。。。看来双向bfs的优化作用实在是很有限呀。

文章作者: 李垚
文章链接: https://blog.ylee.cn/2022/09/06/bfs/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 李垚 !
leetcode
评论
  目录