动态规划

动态规划的基础类题目

• 斐波那契数列
• 背包问题
• 爬楼梯
• ……
• 股票问题
• 子序列问题

使用动态规划解题时需要注意的点：

1.DP数组的定义和下标的含义
2.递推公式
3.DP数组的初始化
4.遍历顺序
5.打印DP数组

动态规划的尝试

• T70.爬楼梯（斐波那契数列）

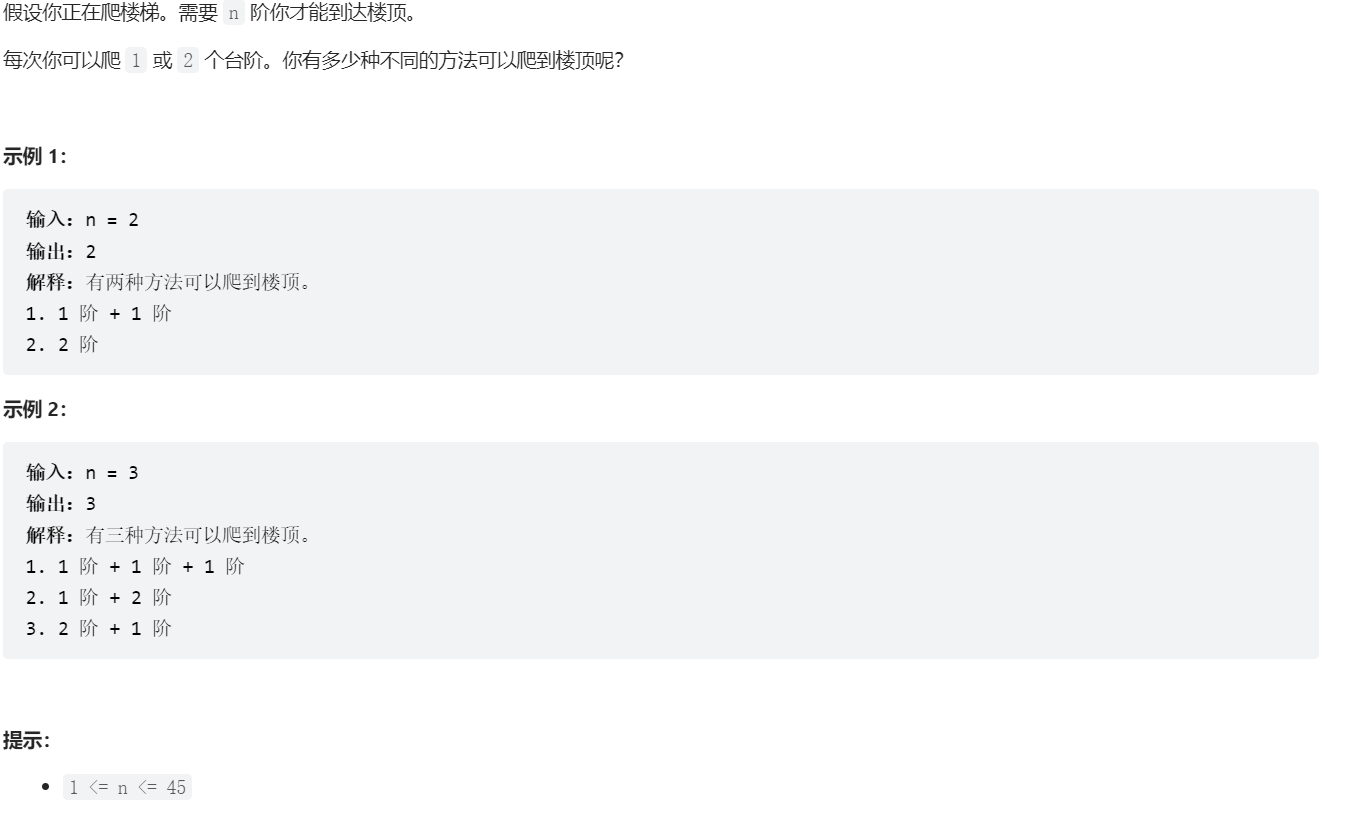
• 题解：

第n级台阶有几种走法，只与第n-1级和第n-2级有关

1.dp数组：dp[i]表示到达i级台阶有dp[i]种方法，
2.递推公式：dp[i] = dp[i-1] + dp[i-2]，
3.dp数组的初始化：dp[0] = 1, dp[1] = 1，
4.遍历顺序：从第n级台阶开始。

//直接使用dp数组
int climbStairs(int n) {
    int dp[n+1];
    dp[0] = 1;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}
//节省部分空间开销的写法
int climbStairs(int n) {
    int dp1 = 1;
    int dp2 = 1;
    int dp = 0;T
    for (int i = 2; i <= n; i++) {
        dp = dp1 + dp2;
        buffer = dp2;
        dp2 = dp1;
        dp1 = dp;
    }
    return dp;
}

• T198.打家劫舍

• 题解：

1. dp数组：dp[i]表示到达i房间时，最大盗取金额，
2. 状态方程：dp[i] = max(dp[i-2] + nums[i], dp[i-1])，意思是，在到达i房间时偷不偷取决于是在这偷了赚的多还是在上一间偷了赚的多，在这一间偷了，赚的钱表示为dp[i-2] + nums[i]，在这一间没偷，赚的钱表示为dp[i-1]，
3. dp数组的初始化：dp[0] = 0, dp[1] = nums[0]，
4. 遍历顺序：从第1房间开始。

   int rob(vector<int>& nums) {
       int dp[nums.size()];
       dp[0] = nums[0];
       dp[1] = max(nums[0], nums[1]);
       for (int i = 2; i < nums.size(); i++) {
           dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
       }
       //当然也可以为了节省内存开销，只储存上一家偷的钱和上上家偷的钱。
       return dp[nums.size()-1];
   }
   

• T213.打家劫舍II

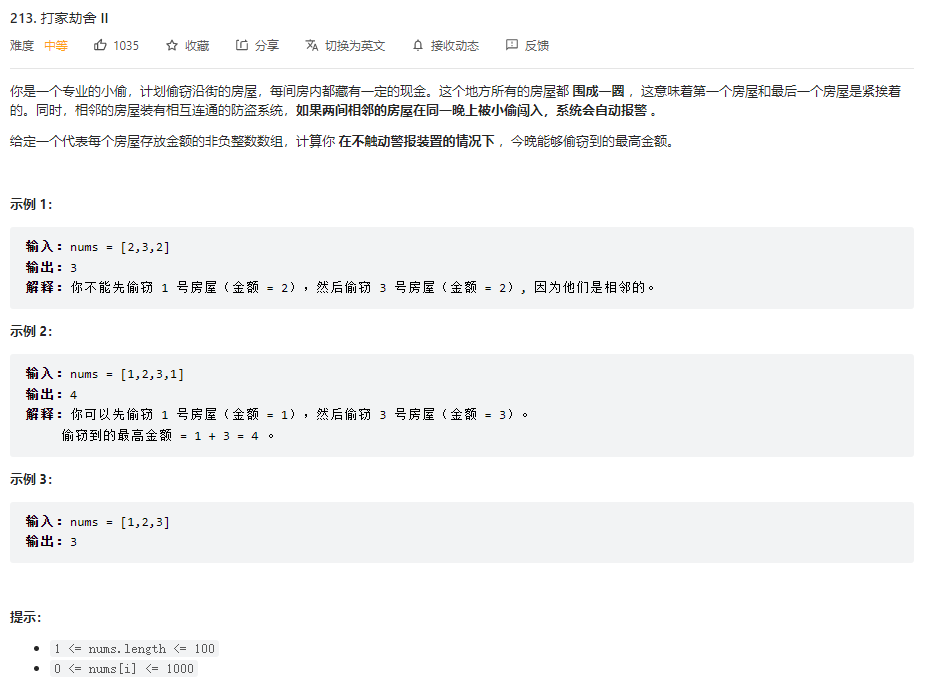
• 题解：

1. dp数组：dp[i]表示到达i房间时，最大盗取金额，
2. 状态方程：dp[i] = max(dp[i-2] + nums[i], dp[i-1])，意思是，在到达i房间时偷不偷取决于是在这偷了赚的多还是在上一间偷了赚的多，在这一间偷了，赚的钱表示为dp[i-2] + nums[i]，在这一间没偷，赚的钱表示为dp[i-1]，
3. dp数组的初始化：这是本题与上题区别较大的地方，在上题中，我们默认在第一间房间偷不偷只取决于在第二间房偷不偷，在这题中，在第一间房偷不偷取决于在最后一间房偷不偷和在上一间房偷不偷，从dp[2]到dp[n-1]的计算方式并不发生变化，存在两种情况，第一间房子不偷，此时最大金额为从第二间偷到第n间的最大金额，最后一间房子偷，此时最大金额为从第一间偷到第n-1间的最大金额，
4. 遍历顺序：从第1房间开始。

int rob(vector<int>& nums) {
    if(nums.size() <= _0) {
        auto max = max_element(nums.begin(), nums.end());
        return *max;
    }
    int dp[nums.size()-1];
    dp[0] = nums[0];
    dp[1] = max(nums[1], nums[0]);
    //从1偷到n-1
    for (int i = 2; i < nums.size()-2; i++) {
        dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        if(i == nums.size()-1){
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }    
    }
    int dp1 = dp[nums.size()-1];
    dp1[0] = nums[1];
    dp1[1] = max(nums[1], nums[2]);
    //从2偷到n
    for (int i = 2; i < nums.size()-2; i++) {
        dp1[i] = max(dp1[i-1], dp1[i-2] + nums[i+1]);
    }
    return max(dp[nums.size()-2], dp1[nums.size()-2]);
}

• T309.买卖股票的最佳时机含冷冻期

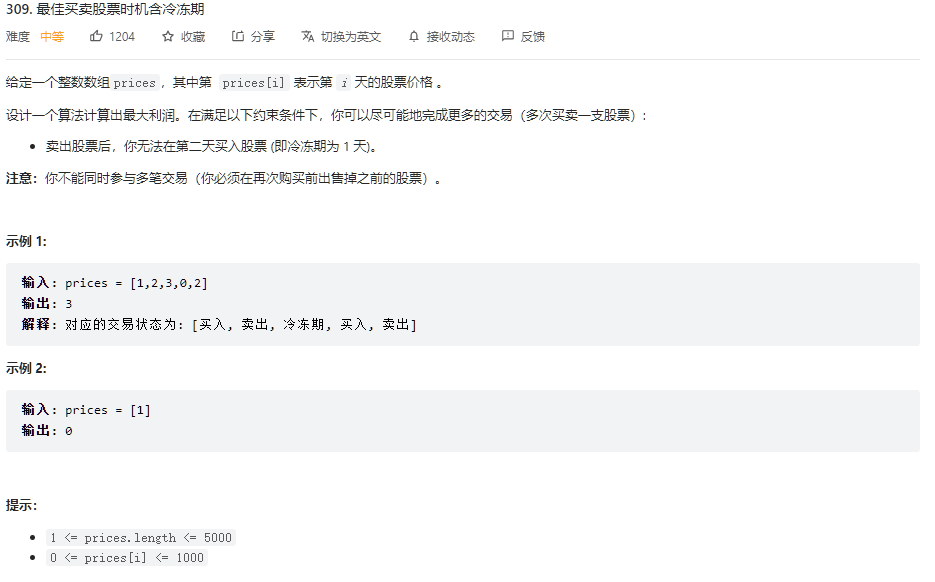
题解：

int maxProfit(vector<int>& prices){
    int len = prices.size();
        if(len <= 1){
            return 0;
        }
        int f0 = -prices[0];
        int f1 = 0;
        int f2 = 0;
        for(int i = 0; i<len; i++){
            int newf0 = max(f0, f2-prices[i]);
            int newf1 = f0 + prices[i];
            int newf2 = max(f2, f1);
            f0 = newf0;
            f1 = newf1;
            f2 = newf2;
        }
        return max(f1, f2);
}