回溯算法

回溯算法

是一种类似于深搜的穷举类型的算法，回溯算法在遍历树的树枝，而深搜则是在遍历树的节点
在解决回溯算法时需要注意的几个问题是：

• 路径：即当前已做出的选择
• 选择列表：即站在当前节点上，可以做出的选择
• 结束条件： 即如何判断已经到达了树的底部，无法再做选择

核心代码

主要的核心操作是在递归调用之前做出选择，将选择从选择列表中删除，在递归之后再撤销已做出的选择。

for option in options:
    # 做出选择
    将该选择从选择列表中移除
    路径.add(option)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(option)
    将该选择重新加入选择列表

回溯算法应用

• T46 全排列

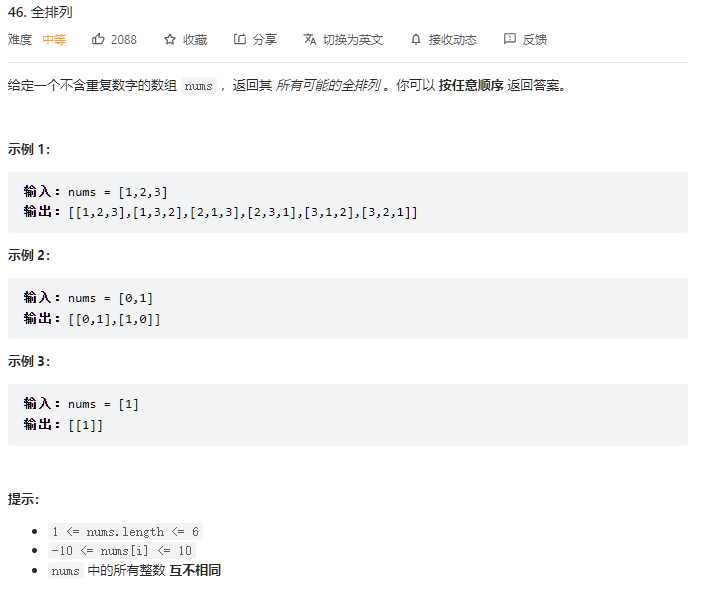
• 题解

void backtrack(vector<int> nums, vector<int>& temp, vector<vector<int>>& ans, vector<bool>& used){
        if(temp.size() == nums.size()){
            ans.push_back(temp);
            return;
        }
        for(int i = 0; i<used.size(); i++){
            if(used[i] == 1) continue;
            used[i] = 1;
            temp.push_back(nums[i]);
            backtrack(nums, temp, ans, used);
            temp.pop_back();
            used[i] = 0;
        }
    }
    vector<vector<int>> permute(vector<int>& nums){
        vector<vector<int>> ans;
        vector<int> temp;
        vector<bool> used(nums.size(), false);
        backtrack(nums, temp, ans, used);
        return ans;    
    }

• T39 组合总和

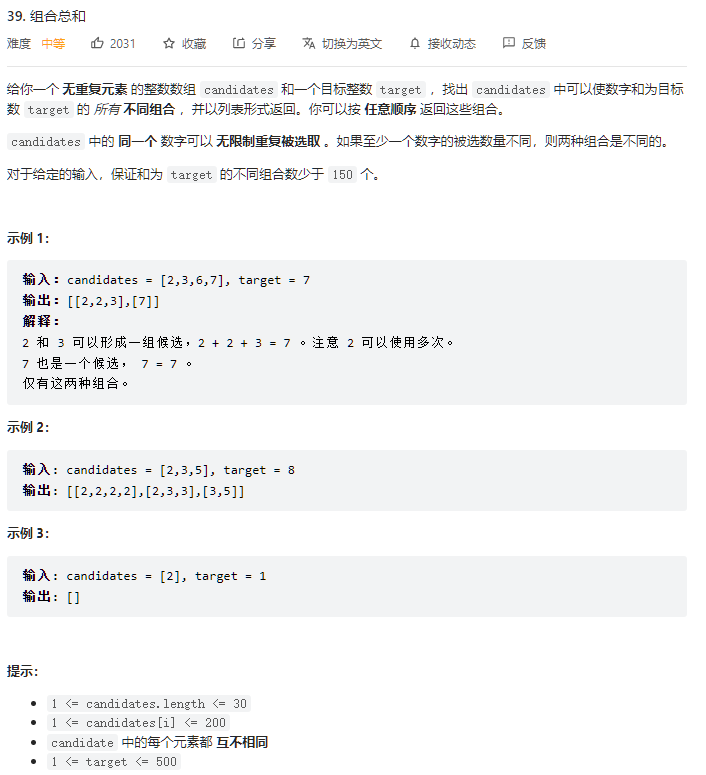
• 题解

  
  void backtrack(vector<int> nums, vector<int>& temp, vector<vector<int>>& ans, int target, int startIndex){
          if(target == 0){
              ans.push_back(temp);
              return;
          }
          if(target < 0){
              return;
          }
          for(int i = startIndex; i<nums.size(); i++){
              target -= nums[i];
              temp.push_back(nums[i]);
              backtrack(nums, temp, ans, target, i);
              // 撤销选择
              target += nums[i];
              temp.pop_back(); 
          }
      }
      vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
          vector<int> temp;
          vector<vector<int>> ans;
          backtrack(candidates, temp, ans, target, 0);
          return ans;
      }
  

• T40 组合总和2

• 题解

void backtrack(vector<int> nums, vector<int>& temp, vector<vector<int>>& ans, vector<bool>& used, int target, int startIndex){
        if(target == 0){
            ans.push_back(temp);
            return;
        }
        if(target < 0){
            return;
        }
        for(int i = startIndex; i<nums.size(); i++){
            // 去重
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            used[i] = 1;
            // if(nums[i] > target) continue;
            temp.push_back(nums[i]);
            target = target - nums[i];
            backtrack(nums, temp, ans, used, target, i+1);
            // 撤销选择
            target += temp.back();
            temp.pop_back();
            used[i] = 0;
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<int> temp;
        vector<vector<int>> ans;
        vector<bool> used(candidates.size(), false);
        sort(candidates.begin(), candidates.end());
        backtrack(candidates, temp, ans, used, target, 0);
        return ans;
    }
    

---

9.20更新，最近又刷了一些回溯算法的题目，感觉难度还是比较大的。写一个回溯算法框架本身不是很难，但是困难的是要怎么用这种相对笨重的算法通过测例。重点还是在于撤销选择和剪枝这两个操作上。之后再做题的话会把这两个操作单独的注释出来。
撤销选择是回溯算法的核心思想，所谓回溯就是撤销选择。
剪枝则是因为回溯算法本质上是dfs遍历，这样导致时间复杂度往往是极高的，就是暴力搜索，很多时候不能直接通过测试，因此使用剪枝来规避一些没有必要的遍历，从而降低时间复杂度。

• T698 划分为k个相等的子集

• 题解

class Solution {
public:
    vector<int> bucket;
    bool backtrack(vector<int>& nums, int k, int cur) {
        if(cur < 0) return true;
        for(int i = 0; i < k; i++) {
            // 剪枝
            if(i > 0 && bucket[i] == bucket[i-1]) continue;
            if(bucket[i] == nums[cur] || bucket[i] - nums[cur] >= nums[0]) {
                // 把当前的数放进第i个桶中
                bucket[i] -= nums[cur];
                if(backtrack(nums, k, cur - 1)) return true;
                // 在这里回溯，不行的话就拿出来
                bucket[i] += nums[cur];
            }
        }
        return false;
    }
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        int len = nums.size();
        int sum = accumulate(nums.begin(), nums.end(), 0);
        if(sum % k != 0) return false;
        int target = sum / k;
        sort(nums.begin(), nums.end());
        if(nums[len - 1] > target) return false;
        vector<int> buffer (k, target);
        bucket.swap(buffer);
        return backtrack(nums, k, len - 1);
    }
};